Question

A uniform cylinder of length L and mass M having cross sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density ρ at equilibrium position. When the cylinder is given a small downward push and released, it starts oscillating vertically with small amplitude. If the force constant of the spring is k, the frequency of oscillations of the cylinder is?

Answer 1

As per the given conditions, you could draw a diagram or a free-body diagram representing all the forces acting on the cylinder. You could equate the net force (F) and also express F as the product of mass and acceleration using Newton’s second law. Now express the acceleration in terms of frequency and hence find the answer.

Formula used:
Hooke’s law,
$F=-kx$
Expression for buoyant force,
${{F}_{B}}=-\rho Vg$

Complete step by step answer:
We are given a uniform cylinder which has a length L, mass M and has a cross-sectional area A which is suspended with its length vertical from a fixed point by a spring that is mass-less. It is also submerged in a liquid of density ρ at equilibrium position. It starts oscillating with small amplitude when a gentle push is given. We are also given the spring constant of the spring as t and we are supposed to find the frequency of oscillations of the cylinder in the question.

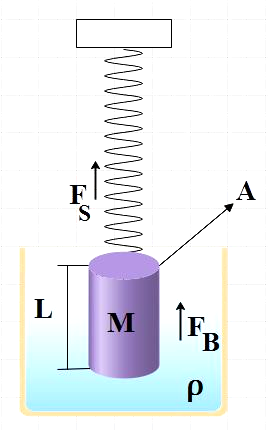
From the above figure, we see the forces acting on the cylinder. There is an upthrust or buoyant force exerted on the cylinder by the liquid and the spring force is also acting during the oscillation. Since both these forces are acting in the upward direction, the net force is given by,
$F={{F}_{B}}+{{F}_{s}}$ …………………….. (1)
Where, ${{F}_{B}}$ is the buoyant force acting on the body given by,
${{F}_{B}}=-\rho Vg$
Where, V is the volume of the water displaced due to the submersion (Archimedes principle) given by,
$V=A\times x$
$\Rightarrow {{F}_{B}}=-\rho Axg$ ………………………….. (2)
${{F}_{s}}$ is the spring force given by Hooke’s law as,
$F=-kx$ ………………………… (3)
Force F exerted on the body now becomes,
$\Rightarrow F=-\left( \rho Axg+kx \right)$
From Newton’s second law,
F=ma
$\Rightarrow Ma=-\left( \rho Axg+kx \right)$
Acceleration due to oscillation is,
$a={{\omega }^{2}}x$
$\Rightarrow M{{\omega }^{2}}x=-\left( \rho Axg+kx \right)$
$\Rightarrow M{{\omega }^{2}}=-\left( \rho Ag+k \right)$
But we have frequency of oscillation ω given by,
$\omega =2\pi f$
$\Rightarrow {{\left( 2\pi f \right)}^{2}}=\left( \dfrac{\rho Ag+k}{M} \right)$
$\Rightarrow f=\dfrac{1}{2\pi }\sqrt{\dfrac{\rho Ag+k}{M}}$
Therefore, the frequency of oscillations of the cylinder is,
$f=\dfrac{1}{2\pi }\sqrt{\dfrac{\rho Ag+k}{M}}$

Note:
You may be wondering about the sign convention used while solving. We have taken the force exerted to push the body into the water as positive and obviously the restoring force as well as buoyant force is acting opposite to this force that is applied and hence negative. Now, while finding the frequency we have taken only the magnitude because, frequency is given by,
$f=\dfrac{1}{2\pi }\sqrt{\left| \dfrac{a}{x} \right|}$