Question

A uniform cube of side $a$ and mass $m$ rests on a rough horizontal table. A horizontal force $F$ is applied normal to one of the faces at a point that is directly above the centre of the face, at a height $\dfrac{3a}{4}$ above the base. The minimum value of $F$ for which the cube begins to tip about the edge is …………. (Assume that cube does not slide)

Answer 1

Hint: The cube is tilted by a force if the torque produced by force is just greater than the torque produced by the gravity about its centre of mass. The torque which acts on the cube equals to $r\times F$.
Formula Used:

Torque $=r\times F$

Complete step by step answer:
When we draw a free body diagram of an object, we find that weight is balanced by normal.

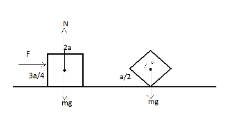
To flip the cube to its tip, torque produced by minimum force is just greater than torque produced by gravity about its centre of mass.
Torque: Torque is the vector quantity means it has both magnitude and direction.
Torque is equals to force multiplied by the perpendicular distance between the force.

Formula of torque is:
Torque $=r\times F$

& {{\tau }_{out}}>{{\tau }_{gravity}} \\\ & F\left( \dfrac{3a}{4} \right)>mg\left( \dfrac{a}{2} \right) \\\ & F>\dfrac{2mg}{3} \\\ \end{aligned}$$ Therefore, the minimum force which will begin to tip about the edge is $$\dfrac{2mg}{3}$$. In this case, the angle between force and distance by which force is acting is $${{90}^{0}}$$ Therefore, Torque $$=r\times F$$ Torque = $$rF\sin \theta $$ $$\theta =\dfrac{\pi }{2}$$ Torque $$=rF$$ Note: In this type of question, first draw the FBD (free body diagram) of the object, and look at which force is balancing out each other. And look at the net effect of the remaining force. The SI unit of Torque (as you can understand by its formula) is Newton metre (Nm).