Solveeit Logo
Login

Question

Question: A uniform conducting wire \(ABC\) lying in a \(XY\) plane has a mass of \(10g\) . A current of \(2A\...

A uniform conducting wire ABCABC lying in a XYXY plane has a mass of 10g10g . A current of 2A2A flows through it. The wire is kept in a uniform magnetic field B=2TB = 2T which acceleration of the wire is:
A. Zero
B. 12m s−212m{\text{ }}{s^{ - 2}} and along the positive Y-axis.
C. 1.2×10−3m s−21.2 \times {10^{ - 3}}m{\text{ }}{s^{ - 2}} along the positive Y-axis.
D. 0.6m s−20.6m{\text{ }}{s^{ - 2}} along the positive X-axis.

Explanation

Solution

In this type of question, first we will find the force due to the magnetic field and then substituting on the formula given by Newton's law we will find the acceleration of the wire. As the magnitude of the field produced will be the same, we can find the answer directly.

Formula used:
f=Blsin⁡θf = Bl\sin \theta
Where,
ff is the force,
BB is the magnetic field,
ll is the length and
ii is the current.

Complete step by step answer:

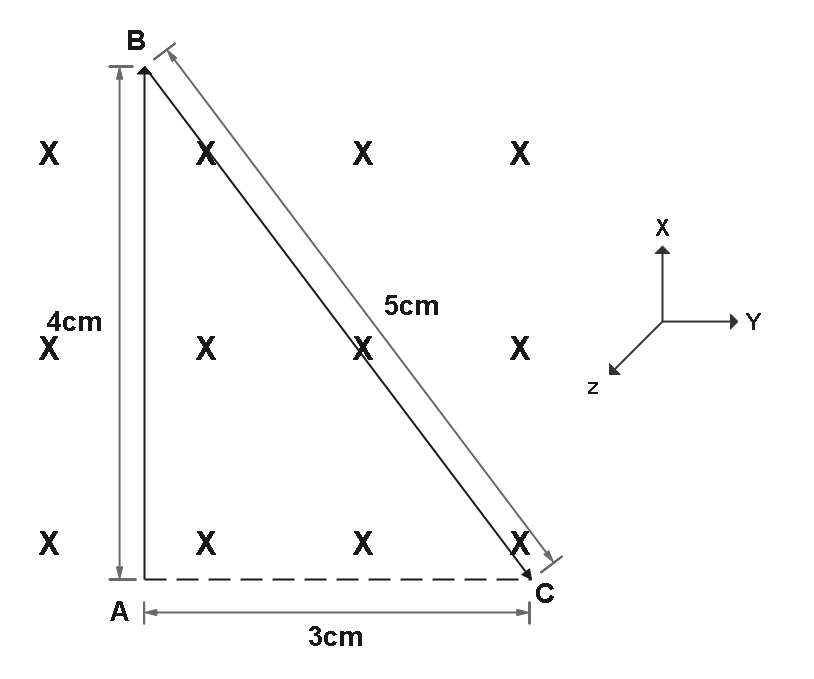
According to the question, it is given that
Mass, m=10gm = 10g
Current, i=2Ai = 2A
Magnetic field, B=2TB = 2T
θ=90∘\theta = {90^ \circ }
And from the figure, AC=3AC = 3
Now, let the force given on ACAC is ff
And we know that,
f=Blsin⁡θf = Bl\sin \theta
Now, substituting the value in above equation,

f=Bilsin⁡θ ⇒f=2×2×3×10−2×sin⁡90∘  f = Bil\sin \theta \\\ \Rightarrow f = 2 \times 2 \times 3 \times {10^{ - 2}} \times \sin {90^ \circ } \\\

⇒f=12×10−2N \Rightarrow f = 12 \times {10^{ - 2}}N (Along Y-axis)
Now we will calculate the acceleration, and we know that
F=ma ⇒a=Fm  F = ma \\\ \Rightarrow a = \dfrac{F}{m} \\\
Now, substituting the value in above equation,
⇒a=12×10−2N10×10−3\Rightarrow a = \dfrac{{12 \times {{10}^{ - 2}}N}}{{10 \times {{10}^{ - 3}}}}
⇒a=12m s−2\Rightarrow a = 12m{\text{ }}{s^{ - 2}} (Along Y-axis)
So, the acceleration is 12m s−212m{\text{ }}{s^{ - 2}} along positive Y-axis
Hence, the correct option is B.

Note:
Take care of units as if you don’t convert the unit in standard format, you can make mistakes and remember that,
F=Bilsin⁡θF = Bil\sin \theta , where. F is force acting on a current carrying conductor is magnetic flux density (magnetic field strength), i is magnitude of current flowing through the conductor, l is length of conductor, θ is angle that conductor makes with the magnetic field.