Question

A uniform circular disk of radius $r$ placed on a rough horizontal plane has initial velocity ${v_0}$ and an angular velocity ${\omega _0}$ as shown. The disc comes to rest after some distance in the direction of motion. Then

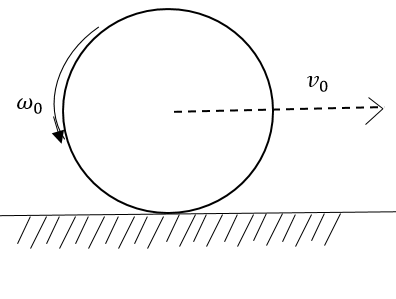
A. The friction force acts in the backwards direction
B. The point of contact of disc with ground has zero velocity
C. ${v_0}$ must be equal to $\dfrac{{r{\omega _0}}}{2}$ in magnitude
D. ${v_0}$ must be equal to $2r{\omega _0}$ in magnitude

Answer 1

When the disc comes to rest, final velocity becomes zero. And there is no force activity on the body to move it further.

Complete step by step answer:
Once, the disc stops. The velocity of the disc becomes zero.
Therefore, from the above explanation the correct option is(B). The point of contact of the disc with ground has zero velocity.
Since, the disc is at rest, there is no force acting on the disc to move it in any direction.
And since, frictional force depends on the external force applied on the disc, the frictional force should also be zero.
Therefore, from the above explanation the incorrect option is(A) The friction force acts in the backwards direction.
We know that linear momentum$= \dfrac{{mw{r^2}}}{2}$
Since, the body is coming to rest,
Linear momentum$=$Angular Momentum.
$\Rightarrow m{v_0}r = \dfrac{{m{w_0}{r^2}}}{2}$
By simplifying it, we get
${v_1} = \dfrac{{{w_0}r}}{2}$
$\Rightarrow {v_1} = \dfrac{{r{w_0}}}{2}$
Therefore, from the above explanation the correct option is (c) ${v_0}$ must be equal to $\dfrac{{r{\omega _0}}}{2}$ in magnitude.
Clearly option (D) ${v_0}$ must be equal to $2r{\omega _0}$ in magnitude is incorrect.

So, the correct answer is “Option B”.

Note:
In multiple correct options, you should check every option for its correctness.
Angular momentum can also be written as $L = Iw$
Where, $L$is angular momentum
$I$is rotational inertia
$w$is angular velocity.