Question

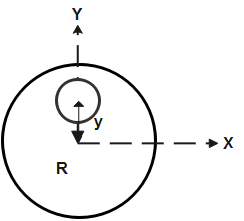
A uniform circular disc of radius R and weight 90N is shown in figure .If small circular portion is cut out, then coordinates of new centre of mass will be (Remaining weight of disc is 65N and$y=\dfrac{3R}{5}$)

Answer 1

Firstly we will calculate the coordinates of centre of mass of the whole disc and centre of mass of the removed disc, then find the mass of the whole disc and removed disc. After finding these values apply the formula for centre of mass for the discrete system by considering both the disc as an individual system.

Complete step-by-step answer:
Since in the given question a uniform circular disc of radius R is given its centre of mass lies at centre which means the origin of X and Y axis.
So Coordinates of centre of mass of Uniform circular disc is $(0,0)$

Let us assume the coordinates of the centre of mass of the circular disc is$({{x}_{1}},{{y}_{1}})$.
$\Rightarrow {{x}_{1}}=0\And {{y}_{1}}=0$ Let us assume the mass of Uniform circular disc is M. So according to the question Weight is given 90N. Since W=Mg Therefore, $M=\dfrac{W}{g}$ So, $M=\dfrac{90}{g}$. Now a small circular portion is removed from the original disc and distance y from the centre of Original disc. So the centre of mass of that small circular portion lies at its geometric centre. Let us assume the coordinates of centre of mass of small circular disc is $({{x}_{2}},{{y}_{2}})$ Since the centre of the Small circle lies at y axis so x- coordinates of centre of mass of small disc becomes 0. $\Rightarrow {{x}_{2}}=0\And {{y}_{2}}=y$ Since value of y is given in the question, $\Rightarrow {{y}_{2}}=y=\dfrac{3R}{5}$
Let us assume the mass of this small circular disc is m.
. So according to the question Weight of the remaining disc is given 65N. Weight (w) of small circular potion is 90-65 = 25 N Since w=mg Therefore, $m=\dfrac{25}{g}$ Assume Original circular disc as one system and small removed circular disc as another system. Let us assume the centre of mass the combined system is $({{X}_{CM}},{{Y}_{CM}})$
Now apply the formula for centre of mass for discrete system,
${{X}_{cm}}=\dfrac{M{{x}_{1}}-m{{x}_{2}}}{M-m}$ & ${{Y}_{cm}}=\dfrac{M{{y}_{1}}-m{{y}_{2}}}{M-m}$ Since ${{x}_{1}}=0\And {{x}_{2}}=0$ then${{X}_{cm}}=0$. Now we calculate coordinates of the centre of mass of the Y axis.
${{Y}_{cm}}=\dfrac{\dfrac{90}{g}\times 0-\dfrac{25}{g}\times \dfrac{3R}{5}}{\dfrac{90}{g}-\dfrac{25}{g}}$ $\Rightarrow {{Y}_{cm}}=\dfrac{-\dfrac{15R}{g}}{\dfrac{65}{g}}$ $\therefore {{Y}_{cm}}=\dfrac{-3R}{13}$. Negative sign shows that the centre of mass of the remaining disc lies on the negative y axis. SO centre of mass of remaining disc is $(0,\dfrac{-3R}{13})$
Note: Centre of mass is that point on the body where the whole mass of the body is supposed to be concentrated. The formula for Centre of mass of discrete system minus is considered when any portion is removed from the original body. Centre of mass always shifts to a heavier portion when some part is removed from the original body.