Question
Question: A uniform circular disc has radius \[R\] and mass \[m\] . A particle also of mass m is fixed at a po...
A uniform circular disc has radius R and mass m . A particle also of mass m is fixed at a point A on the wedge of the disc as in fig. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance 4R from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. It is then allowed to fall so that it starts rotating about PQ. If the linear speed of the particle as it reaches its lowest position is v=xgr. Find x.
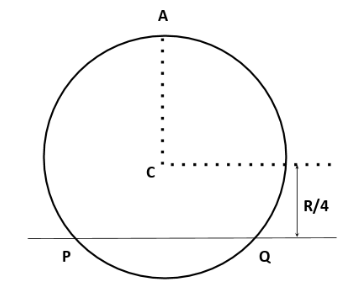
Solution
The given uniform circular disc is initially at rest. Even though the object is at rest, it has some amount of energy stored in it. It is called Potential energy. Then, the disc starts moving in the same plane and rests at final position. When the object starts moving in a certain direction, then the Potential energy is converted into Kinetic energy.
Formula Used:
The Potential energy of a body is given as: PE=mgh
where, m is the mass of the object, g is acceleration due to gravity and h is the height of the object.
The Kinetic energy of a body is given as: KErotational=21Iω2
where, I is the moment of inertia and ω is the angular momentum.
The moment of inertia can be written as I=mK2 where, K is the radius of gyration.
Complete step by step answer:
The given uniform circular disc has radius R and mass m. Also, a particle of mass mis placed at point A. The component of weight of the circular disc and the particle will be W1=mg and W2=mgrespectively. The component of weight will act vertically downwards.
Initially the disc is held vertical with the point A at its highest position. At this point, the disc will have potential energy. When it is then allowed to fall so that it starts rotating about PQ, the potential energy will be converted into rotational kinetic energy. This can be written as
∣PE∣=∣KErotational∣ →(1)
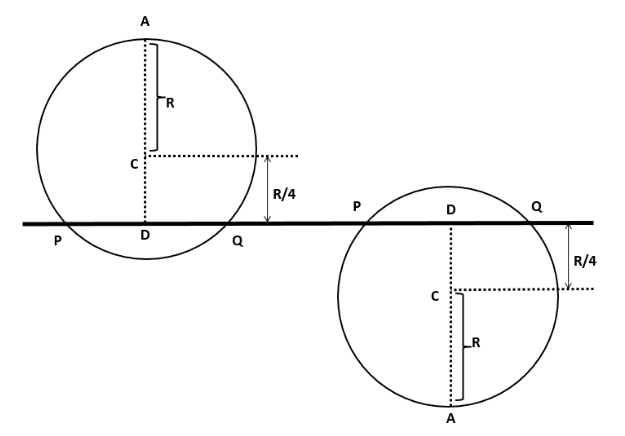
Consider the diagram. (It is the initial position of the disc). Let hparticlebe the height of the particle on the disc from the
hparticle=R+4R=45R
This is the distance of the particle from the fixed horizontal chord PQ.
Then, the Potential energy of the particle will be
PEparticle=mg(45R) →(2)
The distance of the centre of mass of the disc from chord PQ is4R.
hdisc=4R
Therefore, its Potential energy will be
PEdisc=mg(4R) →(3)
Thus from equation (2) and equation (3), the total potential energy in initial position will be
\Rightarrow P{E_{initial}} = mg\left( {\dfrac{{5R}}{4}} \right) + mg\left( {\dfrac{R}{4}} \right) \\\ \Rightarrow P{E_{initial}} = mg\left( {\dfrac{{6R}}{4}} \right) \\\ \Rightarrow P{E_{initial}} = mg\left( {\dfrac{{3R}}{2}} \right)$$ $$ \to (4)$$ Consider the diagram when the disc is in its final position (the second half of the diagram). The height of the particle and the disc from the cord are still the same. But, the potential energy will be negative since the height of the disc is below the chord PQ. Thus, $$P{E_{particle}} = - mg\left( {\dfrac{{5R}}{4}} \right)$$ and $$P{E_{disc}} = - mg\left( {\dfrac{R}{4}} \right)$$ The total potential energy in the final position will be $$P{E_{final}} = - mg\left( {\dfrac{{5R}}{4}} \right) + \left[ { - mg\left( {\dfrac{R}{4}} \right)} \right] \\\ \Rightarrow P{E_{final}} = - mg\left( {\dfrac{{3R}}{2}} \right)$$ $$ \to (4)$$ The magnitude of Potential energy will be $$\left| {PE} \right| = P{E_{final}} - P{E_{initial}} \\\ \Rightarrow\left| {PE} \right| = - mg\left( {\dfrac{{3R}}{2}} \right) - mg\left( {\dfrac{{3R}}{2}} \right) \\\ \Rightarrow\left| {PE} \right| = - mg\left( {\dfrac{{6R}}{2}} \right) \\\ \Rightarrow\left| {PE} \right| = - mg\left( {3R} \right)$$ Therefore, $$\left| {PE} \right| = 3mgR$$ $$ \to (5)$$ The rotational kinetic energy is given as $$\left| {K{E_{rotational}}} \right| = \dfrac{1}{2}I{\omega ^2}$$ where, $$I$$ is the moment of inertia and $$\omega $$ is the angular momentum. Thus, equation (1) can be written as $$3mgR = \dfrac{1}{2}I{\omega ^2}$$ $$ \to (6)$$ The moment of inertia can be written as $$I = m{K^2}$$ where, $$K$$ is the radius of gyration. In the case of particle located at point A, radius of gyration is, $$K = R + \dfrac{R}{4} \\\ \Rightarrow K = \dfrac{{5R}}{4}$$ Thus, $${I_{particle}} = m{\left( {\dfrac{{5R}}{4}} \right)^2} \Rightarrow{I_{particle}} = m\left( {\dfrac{{25{R^2}}}{{16}}} \right) \Rightarrow{I_{particle}} = \dfrac{{25m{R^2}}}{{16}}$$ $$ \to (7)$$ In case of the disc, the moment of inertia will be $${I_{disc}} = m{\left( {\dfrac{R}{4}} \right)^2} \\\ \Rightarrow{I_{disc}} = \dfrac{{m{R^2}}}{4}$$ $$ \to (8)$$ Therefore, $${I_{total}} = {I_{particle}} + {I_{disc}} \\\ \Rightarrow{I_{total}} = \dfrac{{25m{R^2}}}{{16}} + \dfrac{{m{R^2}}}{4} \\\ \Rightarrow{I_{total}} = \dfrac{{29m{R^2}}}{{16}}$$ Thus, equation (6) will be3mgR = \dfrac{1}{2}\left( {\dfrac{{29m{R^2}}}{{16}}} \right){\omega ^2} \\
\Rightarrow {\omega ^2} = \dfrac{{16 \times 2 \times \left( {3mgR} \right)}}{{29m{R^2}}} \\
\Rightarrow{\omega ^2} = \dfrac{{32g}}{{29R}} \\
\therefore \omega = \sqrt {\dfrac{{32g}}{{29R}}} \\
\sqrt {xgR} = \sqrt {\dfrac{{50Rg}}{{29}}} \\
\therefore x = \dfrac{{50}}{{29}} $$
Hence, the value of x is 2950.
Note: Since, here the circular disc is moving, it will be a rotational motion. Therefore, the Kinetic energy associated with this motion will be the rotational Kinetic energy.In the final position of the disc, the potential energy is given negative. This is because the height of the disc is below the chord PQ. The potential energy at rod PQ will be zero.
