Question

A uniform chain of length L is lying on the horizontal table. If the coefficient of friction between the chain and the table top is$\mu$, what is the maximum length of the chain that can hang over the edge of the table without disturbing the rest of the chain on the table?

& A.\,\dfrac{L}{(1+\mu )} \\\ & B.\,\dfrac{\mu L}{(1+\mu )} \\\ & C.\,\dfrac{L}{(1-\mu )} \\\ & D.\,\dfrac{\mu L}{(1-\mu )} \\\ \end{aligned}$$

Answer 1

The horizontal force with which the chain is held on the table equals the weight of the chain hanging from the top of the table. The net force acting downwards on the chain placed on the table equals the product of the mass of the chain present on the table and the acceleration due to gravity.

Complete step by step answer:
From the given information, we have the data as follows.
A uniform chain of length L is lying on the horizontal table. If the coefficient of friction between the chain and the table top is$\mu$.
Let l’ be the length of the chain hanging from the top of the table and ${{M}_{1}}$ be the weight of the chain hanging from the top of the table and ${{M}_{2}}$ be the weight of the chain placed on the top of the table.
Consider the diagram representing the given situation.

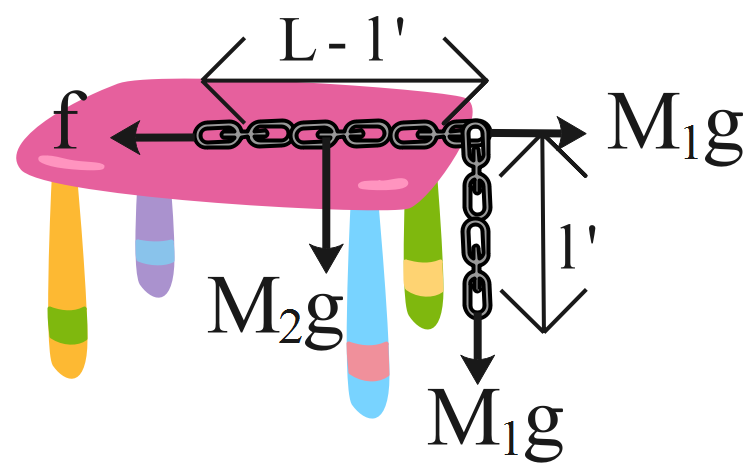
The mass of the chain hanging from the top of the table is given by the formula as follows.
${{M}_{1}}=M\times \dfrac{l'}{L}$
The mass of the chain placed on the top of the table is given by the formula as follows.
${{M}_{2}}=M\left( \dfrac{L-l'}{L} \right)$
The horizontal force with which the chain is held on the table equals the weight of the chain hanging from the top of the table.
The mathematical representation of the same is given as follows.
$f={{M}_{1}}g$
The net force acting downwards on the chain placed on the table equals the product of the mass of the chain present on the table and the acceleration due to gravity.
The mathematical representation of the same is given as follows.
$N={{M}_{2}}g$
The product of the coefficient of friction and the normal force equals the horizontal force with which the chain is held on the table.
$\mu {{M}_{2}}g={{M}_{1}}g$
Substitute the expressions of the masses of the chain in the above equation.
$\mu \left[ M\left( \dfrac{L-l'}{L} \right) \right]g=\left( M\times \dfrac{l'}{L} \right)g$
Cancel out the common terms and represent the above equation in terms of the maximum length of the chain.

& \mu \left( \dfrac{L-l'}{L} \right)=\left( \dfrac{l'}{L} \right) \\\ & \Rightarrow \mu L-\mu l'=l' \\\ & \Rightarrow \mu L=(1+\mu )l' \\\ & \therefore l'=\dfrac{\mu }{1+\mu }L \\\ \end{aligned}$$ $$\therefore $$ The maximum length of the chain that can hang over the edge of the table without disturbing the rest of the chain on the table is $$\dfrac{\mu L}{(1+\mu )}$$. **So, the correct answer is “Option B”.** **Note:** The product of the coefficient of friction and the normal force equals the horizontal force with which the chain is held on the table. The product of the coefficient of friction and the normal force equals the horizontal force with which the chain is held on the table.