Question

A uniform chain of length $L$ and mass $M$ is lying on a smooth table and one third of its length is hanging vertically down over the edge of the table. If $g$ is acceleration due to gravity, work required to pull the hanging part on to the table is
A. $mgL$
B. $\dfrac{{mgL}}{3}$
C. $\dfrac{{mgL}}{9}$
D. $\dfrac{{mgL}}{{18}}$

Answer 1

In this problem, $\dfrac{1}{3}$ rd of the chain is hanging vertically downward from the table. Work will be done by gravity in pulling the chain downwards. The work done will be given as the force applied on the body multiplied by the distance moved due to the force.

Formulae used:
$F = m \times a$
where $F$ is the force, $m$ is the mass of the body and $a$ is the acceleration of the body.
$W = F.d\cos \theta$
where $W$ is the work done, $F$ is the force, $d$ is the displacement caused by the force $F$ and $\theta$ is the angle between the force and displacement vectors.

Complete step by step answer:
According to the given question, $\dfrac{1}{3}$ of the chain is hanging from the table. Let the total length of the chain be $L$ and the total mass of the chain be $m$.We know that the mass is linearly divided, so the mass of the hanging part becomes,
${m_h} = \dfrac{1}{3}m$

Also, we know that when the chain will move to the table, we will have to consider the movement of the centre of mass of the hanging chain. (We cannot consider the movement of each part individually as it is a very time consuming process, hence we consider the centre of mass as a point object where the total mass of the chain is considered)

The length of the hanging part is $\dfrac{L}{3}$ , and the mass is linearly divided, hence the centre of mass is present in the middle of the hanging part. Thus, the distance of the centre of mass from the top of the table $COM = \dfrac{{\dfrac{L}{3}}}{2} = \dfrac{L}{6}$

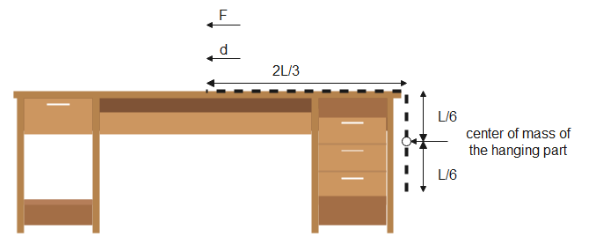
Now, to find the work done, we use the work done formula
$W = Fd\cos \theta$
We can see that the angle between the displacement and force is zero, hence $\cos 0^\circ = 1$
Substituting this value in the above equation, we get
$\Rightarrow W = Fd$ ----------(i)
Now, to calculate the force, we have
$F = ma$
We know that the acceleration here is acceleration due to gravity $g$ and mass is ${m_h}$.

Thus, the equation becomes
$\Rightarrow F = {m_h}g$
Substituting the value of ${m_h}$ , we get
$\Rightarrow F = \dfrac{1}{3}mg$ --------------(ii)
From the above figure, we can see the displacement will be equal to
$d = \dfrac{L}{6}$ --------------(iii)
Substituting the value of equation (ii) and (iii) in equation (i), we get
$\Rightarrow W = \dfrac{1}{3}mg \times \dfrac{L}{6} \\\ \therefore W = \dfrac{{mgL}}{{18}} \\\$
Thus, the correct answer is option D.

Note: Here, we did not consider frictional forces. But in real life, the force applied to pull this chain up will have to be $\dfrac{1}{3}mg + total{\kern 1pt} {\kern 1pt} frictional{\kern 1pt} {\kern 1pt} force$ . Also, the friction will keep on increasing as more and more part of the chain starts coming in contact with the table.