Question

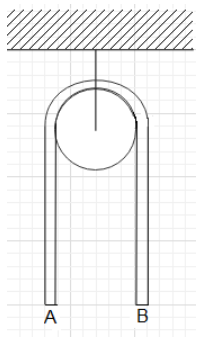
A uniform chain of length 2L is hanging in equilibrium position. If end B is given a slightly downward displacement, the imbalance causes an acceleration. Here pulley is small and smooth and string is extensible. The acceleration of end B when it has been displaced by distance x, is :

$\text{A}\text{. }\dfrac{x}{L}g$
$\text{B}\text{. }\dfrac{2x}{L}g$
$\text{C}\text{. }\dfrac{x}{2}g$
$\text{D}\text{. }g$

Answer 1

Find the gravitational force on the ends A and B when the chain is displaced by a length x. The gravitational forces on the end points will pull the chain downwards and the tension in the chain will try to pull the ends points upwards. Then draw the free body diagrams of both sides of the chain. Find the net forces on both the ends and find the acceleration of end B.
Formula used:
F = mg
${{F}_{net}}=ma$

Complete answer:
It is given that the pulley is small. Therefore, the length of the chain on the both sides of the pulley is equal to L. When the end B of the chain is displaced by a small length, the mass of the right side is greater than the mass on the left side. As a result, the gravitational force on the right side is greater than the gravitational force on the left. Due to this imbalance, the chain accelerates over the pulley. The end B accelerates downwards and the end A accelerates with the same magnitude in the upward direction.
Let find the acceleration of the end B when its displacement is x.
When the chain is displaced by length x. The length of the chain on the right is (L+x) and its length on the left side is (L-x). Therefore, if the mass of the whole chain is M then the mass on the right is $\left( \dfrac{L+x}{2L} \right)M$ and the mass on the left is $\left( \dfrac{L-x}{2L} \right)M$.
The gravitational force on a body of mass m is given as F = mg, where g is acceleration due to gravity.
Therefore, the gravitational forces on the ends B and A are ${{F}_{B}}=\left( \dfrac{L+x}{2L} \right)Mg$ and ${{F}_{A}}=\left( \dfrac{L-x}{2L} \right)Mg$ respectively.
The tension in the chain will try to pull both ends upwards. Let the tension in the chain be T.
Therefore, the free body diagram of the ends B and A are as shown below.

The net force of the end B is ${{F}_{B,net}}=\left( \dfrac{L+x}{2L} \right)Mg-T$.
And the net force of the end A is ${{F}_{A,net}}=T-\left( \dfrac{L-x}{2L} \right)Mg$.
From Newton’s second law of motion, we know that ${{F}_{net}}=ma$, where a is acceleration of the body.
Therefore,
$\left( \dfrac{L+x}{2L} \right)Mg-T=\left( \dfrac{L+x}{2L} \right)Ma$ …… (i).
And
$T-\left( \dfrac{L-x}{2L} \right)Mg=\left( \dfrac{L-x}{2L} \right)Ma$ ……. (ii).
From (ii) we get that
$T=\left( \dfrac{L-x}{2L} \right)Ma+\left( \dfrac{L-x}{2L} \right)Mg$.
Substitute the value of T in (i).
$\Rightarrow \left( \dfrac{L+x}{2L} \right)Mg-\left( \left( \dfrac{L-x}{2L} \right)Ma+\left( \dfrac{L-x}{2L} \right)Mg \right)=\left( \dfrac{L+x}{2L} \right)Ma$
$\Rightarrow \left( \dfrac{L+x}{2L} \right)Mg-\left( \dfrac{L-x}{2L} \right)Ma-\left( \dfrac{L-x}{2L} \right)Mg=\left( \dfrac{L+x}{2L} \right)Ma$
$\Rightarrow \left( \dfrac{L+x}{2L} \right)g-\left( \dfrac{L-x}{2L} \right)a-\left( \dfrac{L-x}{2L} \right)g=\left( \dfrac{L+x}{2L} \right)a$
$\Rightarrow \left( \dfrac{L+x}{2L} \right)g-\left( \dfrac{L-x}{2L} \right)g=\left( \dfrac{L+x}{2L} \right)a+\left( \dfrac{L-x}{2L} \right)a$
$\Rightarrow \left( \dfrac{2x}{2L} \right)g=\left( \dfrac{2L}{2L} \right)a$
$\Rightarrow a=\dfrac{x}{L}g$.
This means that the acceleration of the end B is $\dfrac{x}{L}g$.

Hence, the correct option is A.

Note:
We can also solve the given problem as shown below.
In the above solution we considered that the two ends were different objects and calculated the net forces on both.
Now let us consider the whole chain as one object. The chain is accelerating while an acceleration ‘a’. The net force on the chain is ${{F}_{net}}={{F}_{B}}-{{F}_{A}}$. The tension forces cancel out each other.
$\Rightarrow {{F}_{net}}=\left( \dfrac{L+x}{2L} \right)Mg-\left( \dfrac{L-x}{2L} \right)Mg$
$\Rightarrow {{F}_{net}}=\left( \dfrac{2x}{2L} \right)Mg=\dfrac{x}{L}Mg$
And
$\Rightarrow {{F}_{net}}=Ma$.
$\Rightarrow \dfrac{x}{L}Mg=Ma$
$\Rightarrow a=\dfrac{x}{L}g$
Here, we can also observe that the internal forces with a body or a system of bodies is zero.