Question

A uniform capillary tube of inner radius $r$ is dipped vertically into a beaker filled with water. The water rises to a height $h$ in the capillary tube above the water surface in the beaker. The surface tension of water is $\sigma$. The angle of contact between water and the wall of the capillary tube is $\theta$. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
A. For a given material of the capillary tube, $h$ decreases with increase in $r$.
B. For a given material of the capillary tube, $h$ is independent of $\sigma$.
C. If this experiment is performed in a lift going up with a constant acceleration, then $h$ decreases.
D. $h$ is proportional to contact angle $\theta$.

Answer 1

Surface tension is a property of fluids. The surface tension of a liquid is defined as the energy or work required in order to increase the surface area of liquid and it is because of intermolecular forces in the particle in that liquid. The most common example of surface tension is insects are able to walk on the surface of water. When a liquid is in contact with a solid surface, the angle between the tangent drawn to the free surface of the liquid and the surface of solid at point of contact measured inside the liquid is termed as angle of contact.

Complete step by step answer:
The experiment is describing capillary rise that means rising of water to a specific height within the capillary tube because of difference in pressure at liquid-air interface. Let us first draw the experimental setup for the experiment conducted.

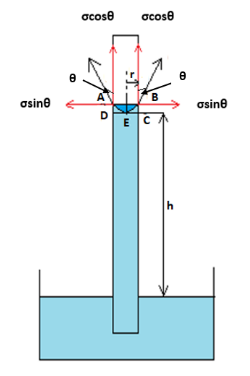
As shown in the diagram above, a uniform capillary tube of inner radius $r$ is dipped vertically into a beaker containing water. A capillary tube is a very small and thin glass tube with a very small inner diameter. The water rises to a height $h$ in the capillary tube above the surface of water in the beaker. The surface tension of water is $\sigma$. The angle of contact between water and the wall of the capillary tube is $\theta$. Now, let us understand the reason for rising water into the capillary tube. The rise of water in capillary tubes without any assistance from external factors is due to cohesive forces, adhesive forces and surface tension of water.
Now, we need to identify the correct options from the given options regarding the capillary rise experiment. For that we first need to consider the section of capillary tube up to which water rises in the tube. At equilibrium, the total upward force of water in the tube due to surface tension of water is given by,
$F = 2\pi r\sigma \cos \theta$……………. (1)
Here, $F$ is the total upward force, $\pi$ is a constant equals to 3.14, $r$ is the inner radius of the capillary tube, $\sigma$ is the surface tension of water and $\theta$ is the angle of contact between water and the inner wall of capillary tube.
The upward force, $F$ is balanced by the weight of water, $W$.
Therefore, weight of the total volume of water is given by,
$W = \pi {r^2}h\rho g$………………..(2)
Here, $W$ is the weight of total volume of water, $h$ is the height of the capillary tube upto which water rises, $\rho$ is the density of water and $g$ is the acceleration due to gravity.
Equating both upward and downward force that is equating equations (1) and (2), we get,
$2\pi r\sigma \cos \theta = \pi {r^2}h\rho g$
$\Rightarrow 2\sigma \cos \theta = hr\rho g$
$\Rightarrow h = \dfrac{{2\sigma \cos \theta }}{{r\rho g}}$
For a given material of the capillary tube, $\theta$ is constant.
So, from the value of $h = \dfrac{{2\sigma \cos \theta }}{{r\rho g}}$, we can conclude that,$h \propto \dfrac{1}{r}$ that means $h$ is inversely proportional to that of $r$.
It means the height of the capillary tube to which water rises, h decreases with increase in the inner radius of the capillary tube, r.
Therefore, option A is the correct option.
For a given metal of capillary tube, $h = \dfrac{{2\sigma \cos \theta }}{{r\rho g}}$, so $h$ is dependent on $\sigma$.
So, option B is incorrect.
If this experiment is performed in a lift going up with a constant acceleration $a$, then, $h' = \dfrac{{2\sigma \cos \theta }}{{r\rho (g + a)}}$. So, clearly it is seen that, $h > h'$.
Here, $a$ is the acceleration whereas $g$ is the acceleration due to gravity.
So, option C is correct.
We know, $h = \dfrac{{2\sigma \cos \theta}}{{r\rho g}}$
So, $h \propto \cos \theta$, i.e., option D is incorrect.

So, correct options are A and C.

Note: We know that water rises in the capillary tube due to cohesive force, adhesive force and surface tension. Let us now understand the meaning of both cohesive and adhesive forces. The adhesive force is the force of attraction between the molecules of water whereas the force of cohesion is the force of attraction between the water molecules and the glass wall of the capillary tube. Also, remember that capillary rise will take place only if adhesive forces are stronger than that of the cohesive forces.