Question

A uniform cable of mass M and length L is placed on a horizontal surface such that its $\dfrac{1}{n}th$ part is hanging below the edge of the surface. To lift the hanging part of the cable up to the surface the work done should be:
$\begin{aligned} & a)\dfrac{MgL}{{{n}^{2}}} \\\ & b)\dfrac{MgL}{2{{n}^{2}}} \\\ & c)\dfrac{2MgL}{{{n}^{2}}} \\\ & d)nMgL \\\ \end{aligned}$

Answer 1

In the question it is given to us that one nth part of the cable is basically hanging about the edge of the horizontal surface on which it is kept. To lift the cable to a height such that the entire cable comes in one line i.e. with respect to the horizontal surface work has to be done against the gravitational pull. Therefore we will calculate the work done by using the expression for gravitational potential energy of the Earth with respect to the initial position of the cable below the horizontal surface.
Formula used:
$U(h)=mgh$

Complete answer:

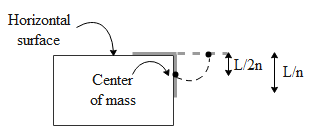
In the above figure we can see that the a section of the cable of length L i.e. L/n part of the cable is hanging below the horizontal surface. In the question it is given to us that the cable has mass M with length L. Hence the mass per unit length of the cable is M/L. The work done(U) in taking a body of mass M to a height h under the action of gravitational pull with respect to its initial position is given by,
$U(h)=mgh$
Now in the above case we can consider this effect to occur about the center of mass of the cable of length L/n. Since the mass is distributed uniformly in the cable we can say that the centre of mass of the cable of length L/n will lie in the middle i.e. at L/2n. Hence we have the work done to bring up the cable to height of L/2n such that the entire cable lies within one line on the surface. The mass (${{M}_{B}}$)of the cable that lies below the edge is equal to,
$\begin{aligned} & {{M}_{B}}=\left( \dfrac{M}{L} \right)\dfrac{L}{n} \\\ & \Rightarrow {{M}_{B}}=\dfrac{M}{n} \\\ \end{aligned}$
Hence the work done to bring the cable to the horizontal surface is,
$\begin{aligned} & U(h)=mgh \\\ & \Rightarrow U(L/2n)=\dfrac{M}{n}g\dfrac{L}{2n} \\\ & \Rightarrow U(L/2n)=\dfrac{MgL}{2{{n}^{2}}} \\\ \end{aligned}$

So, the correct answer is “Option B”.

Note:
In the question it is given to us that the mass is distributed uniformly along the length of the cable. In such a case if we want to find the mass of any given section such that we know the length of the cable is given by the product of mass per unit length times the length of the particular section. One more point to be noted is that mechanical effects taking place on a body can be considered to be the effect on the center of mass of that body.