Question
Question: A uniform but time varying magnetic field is present in a circular region of radius \[R\]. The magne...
A uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnetic field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure. The magnitude of induced emf across the rod is:
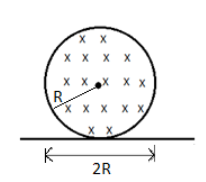
Solution
According to the Faraday’s law, emf induced in a closed loop is equal to the rate of change of magnetic flux. Here, since the magnetic field is varying at the rate of α, an electric field is also generated. Hence, induced emf is also equal to the closed integral of the electric field. Place conducting rods of equal length. Then, the potential difference across the rods will be equal to the induced emf. Thereby, we can derive the equation for induced emf in terms of flux change and potential difference. Also, we know that the rate of change of magnetic flux is equal to the product of rate of change of magnetic field and area. By using all the above equations we can find the emf across the conducting rod.
Formula used:
e=−dtd(ϕB)
e=∮E⋅dl
ϕB=∫B⋅dA=∫BAcosθ
−ΔV=∮E⋅dl
Complete answer:
Given that,
Rate of change of magnetic field,dtdB=α
According to Faraday's law, emf induced in a closed loop is equal to the rate of change of magnetic flux.
i.e.,
For a closed loop, emf induced, e=−dtd(ϕB)----------1
Where,
ϕBis the magnetic flux.
An electric field is also generated due to a varying magnetic field, which is non conservative.
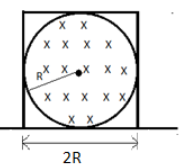
Now, let’s place conducting rods of same length 2Ron all sides of the sphere.
The induced emf in closed loop is given by,
e=∮E⋅dl ------------- 2
Where,
Eis the electric field.
The potential difference across the rods will be equal to the induced emf.
Then, equation 2 becomes,
−ΔV=∮E⋅dl
ΔVis the potential difference.
Then, equation 2 becomes,
−ΔV=dtd(ϕB) ----------------3
We have,
ϕB=∫B⋅dA=∫BAcosθ ----------4
Ais the area of the closed loop.
Here, direction of area is outside the plane of the loop and, given that the magnetic field is perpendicular and into the plane of the loop.
Therefore,
θ=180∘
Then,
ϕB=∫BAcos180
Here, the magnetic field is uniform at any given point of time.
Therefore, equation 4 becomes,
ϕB=−B∫A
We have, area of the sphere, A=πR2 Then,
ϕB=−BπR2 ----------- 5
Where,
R is the radius of the sphere.
Then, substitute 5 in equation 3, we get,
−ΔV=−dtd(BπR2)=−πR2dtdB
Substitute dtdB=αin the above equation
ΔV=πR2α
This is the potential difference across square loop, then potential difference across one rod,
ΔV=4πR2α
Then,
e=4πR2α
Therefore, the magnitude of induced emf across the rod ise=4πR2α
Note:
Outside the loop there is no emf present, but the induced electric field is present. The integral form of Faraday's law is valid even if no conductor is present in the region. The induced electric field produced by a changing magnetic field is non conservative by nature.
