Question

A uniform but time-varying magnetic field $B(t)$ exists in a circular region of radius $a$ and is directed into the plane of the paper, as shown in the figure. The magnitude of the electric field at point $P$ at a distance $r$ from the centre of the circular region:

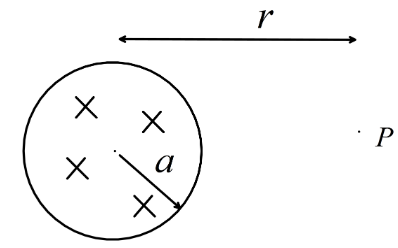
A. is zero
B. decreases as $\dfrac{1}{r}$
C. increases as $r$
D. decrease as $\dfrac{1}{{{r^2}}}$

Answer 1

Lenz’s states that the current induced in a circuit due to a change in a magnetic field is directed to oppose the change in flux and to exert a mechanical force which opposes the motion. Mathematical expression of the Lenz’s law is given by, $V = - \dfrac{{d\phi }}{{dt}}$ where, $\phi$ is the magnetic flux passing through the surface $V$ is the emf across the loop. The electric field is related to emf as, $V = - \oint {\vec E \cdot d\vec l}$. Where, $\vec E$ is the electric field of the region and $d\vec l$ is the path element.

Complete step by step answer:
The magnetic flux through the loop can be calculated from, $\phi = \vec B \cdot \vec A$ where the surface area of the loop. Here, we have given here a region with magnetic field $B(t)$, within the radius $a$ and the direction of it is into the plane of the paper. Now, we have to find the electric field at a distance $r$ from it. Now, potential difference is related to the electric field as $V = - \oint {\vec E \cdot d\vec l}$. Where, $\vec E$ is the electric field of the region and $d\vec l$ is the path element and integration is along the path.

Now, we have here a magnetic field $B(t)$, hence, flux will be, $\phi = \vec B(t) \cdot \vec A = B(t)A$since the angle between the magnetic field and the surface is zero. So, emf will be, $V = - \dfrac{{d\phi }}{{dt}} = - A\dfrac{{dB(t)}}{{dt}}$ since, surface area is constant.
$V = - \pi {a^2}\dfrac{{dB(t)}}{{dt}}$
Now, at a distance $r$the emf will be in terms of the electric field at P,
$V = - \oint {\vec E \cdot d\vec l}$.
$\Rightarrow V = - E\oint {dl}$ Since the electric field will be uniform in the region $r \geqslant a$ due to the magnetic field.
$V = - E\left( {2\pi r} \right)$
So, equating both the equations we get,
$- E\left( {2\pi r} \right) = - \pi {a^2}\dfrac{{dB(t)}}{{dt}}$
$\Rightarrow E\left( {2\pi r} \right) = \dfrac{1}{r}\dfrac{{{a^2}}}{2}\dfrac{{dB(t)}}{{dt}}$
$\therefore E = \dfrac{1}{r}\dfrac{{{a^2}}}{2}\dfrac{{dB(t)}}{{dt}}$
So, at an instant of time the electric field will be inversely proportional to the distance of the point $P$. So, $E \propto \dfrac{1}{r}$. Hence, the magnitude of the electric field at point $P$ at a distance $r$ from the centre of the circular region decreases as $\dfrac{1}{r}$.

Hence, option B is correct.

Note: The electric field at the point P is not a constant of time it varies as the slope of the magnetic field varies with time. If the slope is uniform then the electric field is also uniform if it is non uniform then the electric field is also non-uniform. For time varying magnetic fields the electric field is given by Maxwell's equation as, $\nabla \times E = \dfrac{{\partial B}}{{\partial t}}$.