Question

A uniform bar of length l and mass m stands vertically touching a vertical wall (y-axis). When slightly displaced, its lower end begins to slide along the floor (x-axis). The expression for the angular velocity (ω) of the bar as a function of θ is given by $\sqrt {\dfrac{{xg(1 - \sin \theta )}}{l}}$. Find the value of x. Neglect the effect of friction everywhere.

Answer 1

Use the concept that the rotating with an angular velocity, $\omega$ about its center of mass. In order to solve the above question, first, we will find the angular velocity of the rod in the horizontal and vertical direction of the rod with respect to the center of mass which will lie at the midpoint of the rod then we will apply the conservation of energy in the horizontal and vertical direction. Finally, we will get the value angular velocity and comparing with the given equation we can determine the value of x.

Complete step by step answer:
Given,
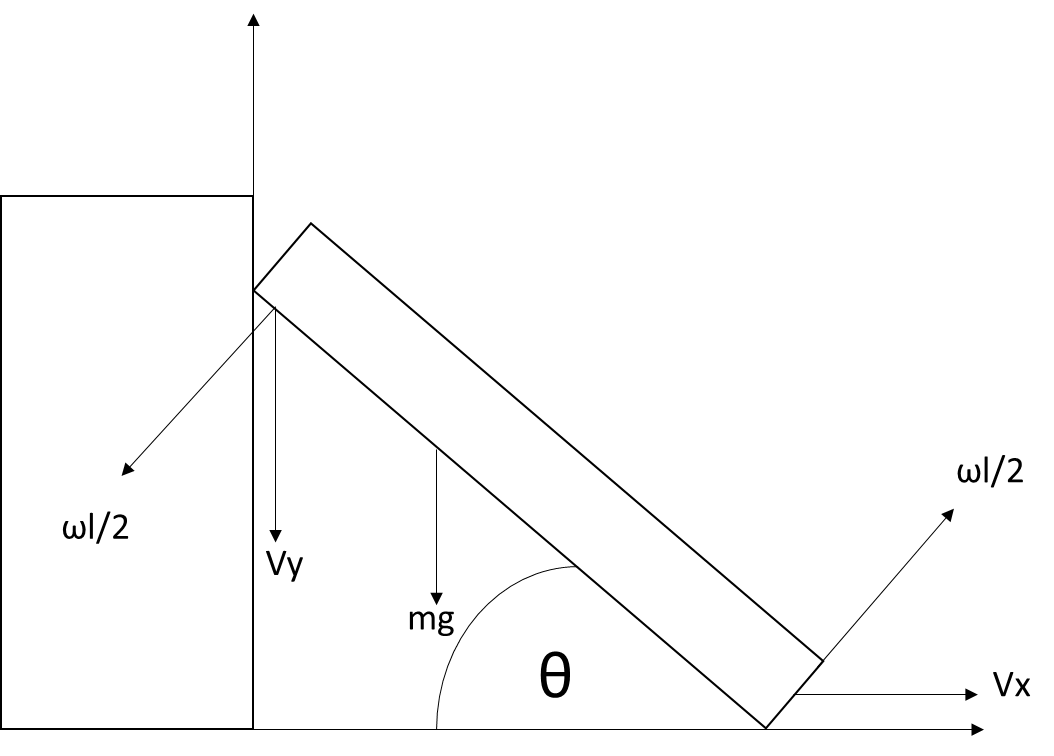
The length of the rod = $l$
Angular velocity of the rod about the center of mass = $\omega$
Length of each end from the center of mass, $r = \dfrac{l}{2}$
Tangential angular velocity of each end about the center of mass is given by
$v = \omega r \Leftrightarrow v = \omega \dfrac{l}{2}$
Let the vertical linear velocity of the rod = ${v_y}$.
Let the horizontal linear velocity of the rod = ${v_x}$.
Let the mass of the rod be $m$.
The lower portion of the rod is moving in a horizontal direction.
So the horizontal velocity ${v_x}$ must be equal to the horizontal component of the tangential angular velocity
$\Rightarrow {v_x} = \dfrac{{\omega l\sin \theta }}{2}$
Similarly, the vertical velocity ${v_x}$ must be equal to the vertical component of the tangential angular velocity
$\Rightarrow {v_y} = \dfrac{{\omega l\cos \theta }}{2}$
Initially, when the rod was vertical its center of mass was at a height of l/2 from the ground.
When the lower end makes an angle of θ with the horizontal.
The center of mass is at a height of $\dfrac{{l\sin \theta }}{2}$
Moreover the rod is rotating about its center of mass so moment of inertia of the rod is
$I = \dfrac{{m{l^2}}}{{12}}$
Now applying energy conservation,
$\text{The energy of rod in vertical position = Energy of the rod}$ when it is at an angle θ with the horizontal.
$\text{Potential energy = Potential energy + linear kinetic energy + rotational kinetic energy}$
$\Rightarrow \dfrac{{mgl}}{2} = \dfrac{{mgl\sin \theta }}{2} + \dfrac{1}{2}m{\left( {\dfrac{{\omega l\cos \theta }}{2}} \right)^2} + \dfrac{1}{2}m{\left( {\dfrac{{\omega l\sin \theta }}{2}} \right)^2} + \dfrac{1}{2}I{\omega ^2}$
On putting the value of moment of inertia, $l$ we get
$\Rightarrow \dfrac{{mgl}}{2} = \dfrac{{mgl\sin \theta }}{2} + \dfrac{1}{2}m{\left( {\dfrac{{\omega l\cos \theta }}{2}} \right)^2} + \dfrac{1}{2}m{\left( {\dfrac{{\omega l\sin \theta }}{2}} \right)^2} + \dfrac{1}{2}\dfrac{{m{l^2}}}{{12}}{\omega ^2}$
On simplification we get
$\Rightarrow \dfrac{{mgl}}{2}(1 - \sin \theta ) = \dfrac{{m{l^2}{\omega ^2}}}{6}$
On solving for $\omega$ we get
$\Rightarrow \omega = \sqrt {\dfrac{{3g(1 - \sin \theta )}}{l}}$
Comparing with the given equation
$\Rightarrow \omega = \sqrt {\dfrac{{xg(1 - \sin \theta )}}{l}}$
$\Rightarrow \therefore x = 3$

Therefore the required value of x is 3.

Note:
We must not consider any friction in this question as the question clearly mentions no friction anywhere if friction was mentioned in the problem in place of energy conservation we must use the work-energy theorem because there will be some work done by the frictional force. Also, take care of the moment of inertia because it is different for different bodies.