Question

A uniform bar of length $6a$ and mass $8m$ lies on a smooth table. Two- point masses $m$ and $2m$ moving in a horizontal plane with speeds $2v$ and $v$ strike the bar as shown and stick to the bar after the collision.
If $\omega$is the angular velocity about the centre of mass, E is the total energy and
${v_c}$ is the velocity of the centre of mass, after collision then:

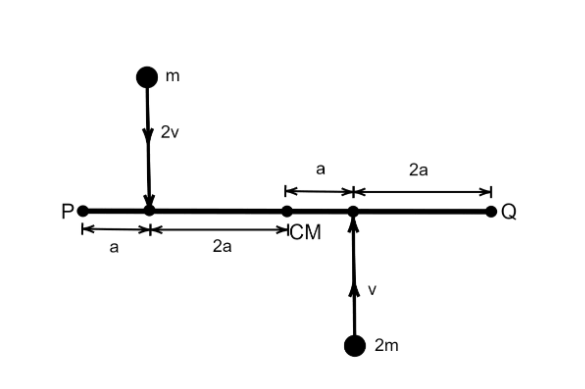
(A) ${v_c} = 0$
(B) ${v_c} = \dfrac{{3v}}{{5a}}$
(C) $E = \dfrac{{m{v^2}}}{5}$
(D) $E = \dfrac{{3m{v^2}}}{5}$

Answer 1

For solving this question, we need to remember conservation laws. Conservation of linear momentum (linear momentum is conserved when there is no external force) and conservation of angular momentum (angular momentum is conserved when there is no external torque).

Complete step by step solution:

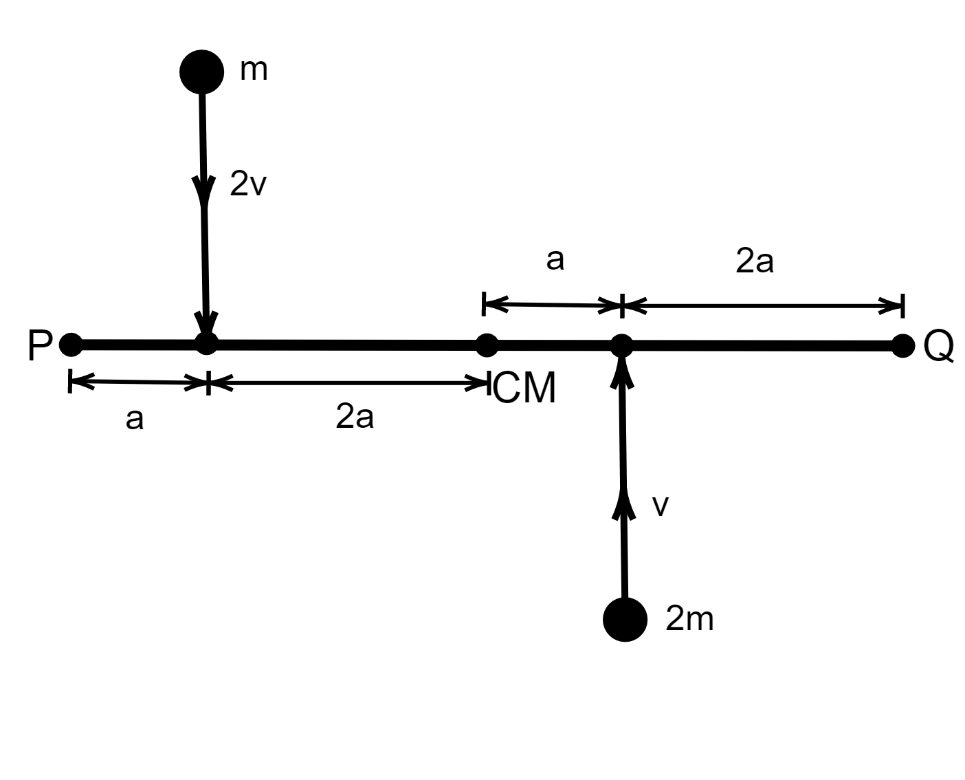
Angular momentum is expressed as:
$\vec L = \vec r \times m\vec v$
where, $\vec r$ is the distance at which the point is colliding to the axis point
$\vec v$ is the velocity of the point.
Or,
$\overrightarrow {\left| L \right|} = mvr\sin \theta$
In this problem for both of the points, we have
$\vec r \bot \vec v$
Thus, angular momentum can be written as
$L = mvr$
According to the law of conservation of angular momentum, we get
${L_i} = {L_f}$ $- - - - (1)$
where, ${L_i}$is the angular momentum before the collision,
${L_f}$is the angular momentum after the collision.
In this problem, ${L_i}$ is given as
${L_i} = {m_1}{v_1}{r_1} + {m_2}{v_2}{r_2}$
where, ${m_1}{v_1}{r_1}$is the angular momentum of the first point with mass $m$and velocity $2v$,
${m_2}{v_2}{r_2}$is the angular momentum of the second point with mass $2m$ and velocity $v$.
$\Rightarrow {L_i} = m(2v)(2a) + (2m)(v)(a)$
$\Rightarrow {L_i} = 2mva + 4mva$
Hence the initial angular momentum is given as
$\Rightarrow {L_i} = 6mva$
Now, we calculate the final angular momentum.
${L_f} = ({I_1} + {I_2} + {I_3})\omega$
where, ${I_1}$ is the moment of inertia of the first point about the centre of mass (cm),
${I_2}$ is the moment of inertia of the second point about cm,
and ${I_3}$ is the moment of inertia of the rod about cm.
We know that, the moment of inertia for a point is given by
$I = m{r^2}$
So, the moment of inertia of the first and second point is given as
$\Rightarrow {I_1} = m{(2a)^2}$
$\Rightarrow {I_2} = 2m{a^2}$
Moment of inertia of a rod about its centre of mass is $\dfrac{{m{l^2}}}{{12}}$.
So, ${I_3} = \dfrac{{(8m) \times {{(6a)}^2}}}{{12}}$
Using the equation$1$, we get
$6mv = \left( {m{{(2a)}^2} + 2m{a^2} + \dfrac{{(8m) \times {{(6a)}^2}}}{{12}}} \right)\omega$
$\Rightarrow 6mv = \left( {4m{a^2} + 2m{a^2} + \dfrac{{8m \times 36{a^2}}}{{12}}} \right)\omega$
Solving this equation, we get
$6mv = \left( {6m{a^2} + 24m{a^2}} \right)\omega$
$\Rightarrow 6mv = 30m{a^2}\omega$
So angular velocity is,
$\omega = \dfrac{v}{{5a}}$.
Now, we look into the conservation of linear momentum, i.e.
$\overrightarrow {{p_i}} = \overrightarrow {{p_f}}$ $- - - - (2)$
Where, $\overrightarrow {{p_i}}$is the initial linear momentum,
$\overrightarrow {{p_f}}$is the final linear momentum.
Initial linear momentum is given by,
$\overrightarrow {{p_i}} = m( - 2\vec v) + 2m\vec v$
$\Rightarrow \overrightarrow {{p_i}} = 0$.
Final momentum is
$\overrightarrow {{p_f}} = M\overrightarrow {{v_c}}$
Where, $M$ is the total mass of the rod and point system,
${v_c}$is the velocity of the centre of mass.
Using the equation $(2)$, we get
$0 = M\overrightarrow {{v_c}}$
$\Rightarrow {v_c} = 0$
Now, the final energy can be calculated as
$E = \dfrac{1}{2}M{v_c}^2 + \dfrac{1}{2}\left( {{I_1} + {I_2} + {I_3}} \right){\omega ^2}$
$\Rightarrow E = 0 + \dfrac{1}{2}\left( {m{{(2a)}^2} + 2m{a^2} + \dfrac{{(8m) \times {{(6a)}^2}}}{{12}}} \right){\left( {\dfrac{v}{{5a}}} \right)^2}$
Solving this, we get
$E = \dfrac{1}{2}\left( {6m{a^2} + 24m{a^2}} \right)\left( {\dfrac{{{v^2}}}{{25{a^2}}}} \right)$
$\Rightarrow E = \dfrac{1}{2}30m{a^2}\dfrac{{{v^2}}}{{25{a^2}}} = \dfrac{{3m{v^2}}}{5}$

Hence, Option (A) and (D) is correct.

Note: While this question is lengthy, one should simply go step by step and use a simple concept. While calculating angular momentum, you should take care of the distance from the axis. Calculating about the wrong axis would ultimately give you the wrong answer.