Question
Question: A uniform bar of length \(6a\) and mass \(8m\) lies on a smooth horizontal table. Two point masses \...
A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v respectively, strike the bar( as shown in figure) and stick to the bar after collision. C represents the centre of mass of the bar. Denoting angular velocity (about the centre of mass), total energy and velocity of centre of mass by ω,E and vc respectively, then after collision we have
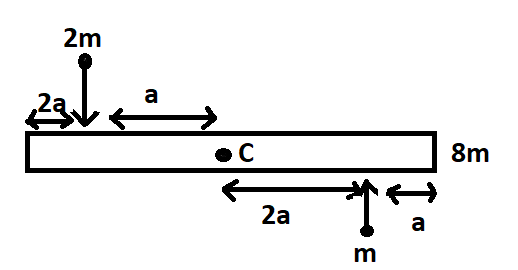
A. vc=0B. ω=5a3vC. ω=5avD. E=53mv2
Solution
- Hint: We will have to calculate each physical quantity to find the correct answer for the given question. The two masses stick to the bar and hence there is no external force or torque on the bar and the conservation laws can be used.
Complete step-by-step solution -
We are given a uniform bar of length 6a and mass 8m which lies on a smooth horizontal table as shown in the figure. There are two masses m and 2m striking the bar with velocities of 2v and v respectively as shown in the figure.
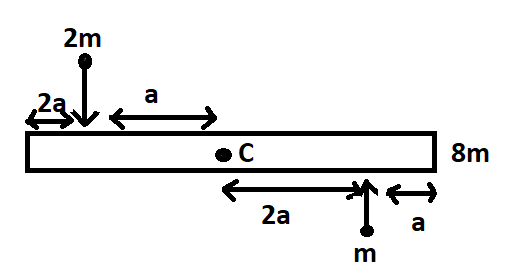
Firstly, the body is experiencing no external force so
Fext=0
Therefore using law of conservation of linear momentum we can write the equation:
(m1+m2+m3)V=m1v1+m2v2+m3v3
(2m+m+8m)vc=−2mv+m×2v+0
11mvc=0
vc=0
Therefore, there is no translatory motion as velocity of centre of mass of the bar is zero
Now since the external torque on the system is also zero i.e.
τext=0
Angular momentum of the system is also conserved. Thus, we will apply the law of conservation of angular momentum on the system
(I1+I2+I3)ω=m1v1r1+m2v2r2
Here, we must use the formula of moment of inertia of a bar when the axis of rotation is perpendicular to bar and through its centre i.e,
Iω=12Ml2
\begin{aligned}
& \left\\{ 2m{{a}^{2}}+m{{(2a)}^{2}}+\dfrac{8m\times {{(6a)}^{2}}}{12} \right\\}\omega =2mva+m(2v)(2a) \\\
& \Rightarrow \left( \dfrac{72m{{a}^{2}}+288m{{a}^{2}}}{12} \right)\omega =6mva \\\
& \Rightarrow \dfrac{360m{{a}^{2}}}{12}\omega =6mva \\\
\end{aligned}
30mωa2=6mva
Cancelling the like terms, we get
⇒ω=5av
This is the rotational velocity of the system.
Now,
Total energy=Rotational energy+Translational energy
(There is no translatory motion since vc=0 )
E=21Iω2
E=21(30ma2)(5av)2
E=53mv2
The correct answers are A. vc=0, C. ω=5av, D. E=53mv2
Note: Students must note that the centre of mass is nothing but a point where the whole mass of the body is concentrated. Also, certain formulas for moment of inertia for a rod, disc, cylinder, sphere should be memorised by the students to use directly in the numerical problems. The various formulas are given as
& {{I}_{rod}}=\dfrac{1}{12}M{{r}^{2}} \\\ & {{I}_{disc}}=\dfrac{1}{2}M{{r}^{2}} \\\ & {{I}_{cylinder}}=\dfrac{1}{2}M{{r}^{2}} \\\ \end{aligned}$$