Question

A uniform bar of length $6a$ and mass $8m$ lies on a smooth horizontal table. Two point masses $m$ and $2m$ moving in the same horizontal plane with speed $2v$ and $v$ respectively, strike the bar(as shown in figure) and stick to the bar after collision. $C$ represents the centre of mass of the bar. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by $\omega, E$ and ${v_c}$ respectively after collision, then:

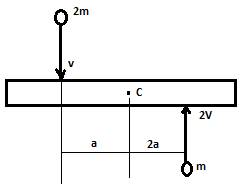
A. ${v_c} = 0$
B. $\omega = \dfrac{{3v}}{{5a}}$
C. $\omega = \dfrac{v}{{5a}}$
D. $E = \dfrac{{3m{v^2}}}{5}$

Answer 1

If a beam of light is struck on a lens then the ability to diverge this beam of light by the lens will depend on the power of the lens and the degree of divergence of the power. We will analyse the possibility of each option here.

Complete step by step answer:
Here we can get the conservation of the angular momentum also.
Given,
Length of the uniform bar= $l = 6a$
Mass of the uniform bar $= 8m$
We will find the total linear momentum of the bar when the two-point masses stick to the bar with their velocities,
So total linear momentum=$m(2v) + 2m( - v) = 0$
This shows that the linear velocity of the centre of mass (COM)of the uniform bar is zero after the collision.
Hence ${v_c} = 0$.
This shows that option (A) is correct. Now we will check for the other options also.
Here we see that the point masses after striking the bar stick to it, that means after striking the bar and two-point masses will act as a single mass of $(8m + 2m + m) = 11m$.
Hence now we can apply the conservation of angular momentum here,
So, applying the conservation of angular momentum to find the angular velocity of the bar after striking the bar,
$(m \times 2v \times 2a) + (2m \times ( - v) \times a) + \left( {\dfrac{{8m{a^2}}}{{12}} \times 0} \right) = (m \times 4{a^2} \times \omega ) + (2m \times {a^2} \times \omega ) + \left( {\dfrac{{8m{a^2}}}{{12}} \times \omega } \right)$
$\Rightarrow 2mva = \left( {6m{a^2} + \dfrac{{2m{a^2}}}{3}} \right)\omega$
$\Rightarrow 2mva = \left( {\dfrac{{20m{a^2}}}{3}} \right)\omega$
$\Rightarrow v = \left( {\dfrac{{10a}}{3}} \right)\omega$
$\Rightarrow \omega = \dfrac{{3v}}{{10a}}$
Thus, we have got the angular velocity.
Total inertia of the system= $\dfrac{{8m{a^2}}}{{12}} + 4m{a^2} + 2m{a^2} = \dfrac{{20m{a^2}}}{3}$
Now we will find the total energy after the collision $= \dfrac{{I{\omega ^2}}}{2}$
Putting the values, we get
$= \dfrac{1}{2}\left( {\dfrac{{20m{a^2}}}{3}} \right){\left( {\dfrac{{3v}}{{10a}}} \right)^2}$
$= \left( {\dfrac{{10m{a^2}}}{3}} \right)\left( {\dfrac{{9{v^2}}}{{100{a^2}}}} \right)$
$= \left( {\dfrac{{3m{v^2}}}{{10}}} \right)$
Hence only option (A) is the correct answer.

Note:
When there is a collision of the two or more objects then there are chances that after they get entangled, they may have both motion, rectilinear motion and the rotational motion. That’s why we have checked here the possibility. We find that the rectilinear motion of the centre of mass is not possible that’s why we have applied the conservation of “angular” momentum not the conservation of “linear” momentum.