Question

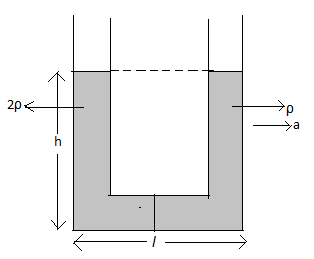
A U-tube of base length ‘$l$’ is filled with the same volume of two liquids of densities $\rho$ and $2\rho$ is moving with an acceleration ‘$a$’ on the horizontal plane. If the height difference between the two surfaces (open to atmosphere) becomes zero then the height $h$ is given by

A. $\dfrac{a}{{2g}}l$
B. $\dfrac{{3a}}{{2g}}l$
C. $\dfrac{a}{g}l$
D. $\dfrac{{2a}}{{3g}}l$

Answer 1

Use the formula of pressure-depth relation. This formula gives the relation between the atmospheric pressure, density of liquid, acceleration of liquid and depth.

Formula used:
The pressure $P$ at a depth $h$ is given by
$P = {P_0} + \rho gh$ …… (1)
Here, ${P_0}$ is the atmospheric pressure, $\rho$ is the density and $g$ is the acceleration due to gravity.

Complete step by step answer:
A U-tube of base length ‘$l$’ is filled with the same volume of two liquids of densities $\rho$ and $2\rho$ which are moving with an acceleration ‘$a$’ on the horizontal plane.
Redraw the diagram of the U-tube.

The liquid with the density $2\rho$ must be moving slowly as compared to the liquid with the density $\rho$.
The liquids have the acceleration $a$ only in the horizontal plane and not in the vertical plane.
Using equation (1), determine the pressure ${P_A}$ at point A considering the right column of the U-tube.
${P_A} = {P_0} + \rho gh$
Using equation (1), determine the pressure ${P_B}$ at point B from point A considering the right column of the U-tube.
${P_B} = {P_A} + \rho a\dfrac{l}{2}$
Substitute ${P_0} + \rho gh$ for ${P_A}$ in the above equation.
${P_B} = {P_0} + \rho gh + \rho a\dfrac{l}{2}$
Using equation (1), determine the pressure ${P_C}$ at point C from point B considering the right column of the U-tube.
${P_C} = {P_B} + 2\rho a\dfrac{l}{2}$
Substitute ${P_0} + \rho gh + \rho a\dfrac{l}{2}$ for ${P_B}$ in the above equation.
${P_C} = {P_0} + \rho gh + \rho a\dfrac{l}{2} + 2\rho a\dfrac{l}{2}$
${P_C} = {P_0} + \rho gh + \dfrac{3}{2}\rho al$ …… (2)
Using equation (1), determine the pressure ${P_C}$ at point C considering the left column of the U-tube.
${P_C} = {P_0} + 2\rho gh$ …… (3)
The height difference between the two surfaces of two liquids open to the atmosphere becomes zero. Hence, the pressure at point C from both right and left liquid columns are the same.
Equate equation (2) and (3).
${P_0} + \rho gh + \dfrac{3}{2}\rho al = {P_0} + 2\rho gh$
$\Rightarrow \dfrac{3}{2}\rho al = \rho gh$
Rearrange the above equation for height $h$.
$h = \dfrac{{\dfrac{3}{2}\rho al}}{{\rho g}}$
$\Rightarrow h = \dfrac{{3a}}{{2g}}l$
Therefore, the height $h$ is $\dfrac{{3a}}{{2g}}l$.

So, the correct answer is “Option B”.

Note:
The pressure-depth relation is not the same for the pressure at the height h.
The height difference between the two surfaces (open to atmosphere) becomes zero.
The average density of a substance or object is defined as its mass per unit volume.