Question
Question: A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two r...
A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two rows are in the same level with 10.0cm of water in one arm and 12.5cm of spirit in the other. What is the specific gravity of spirit?
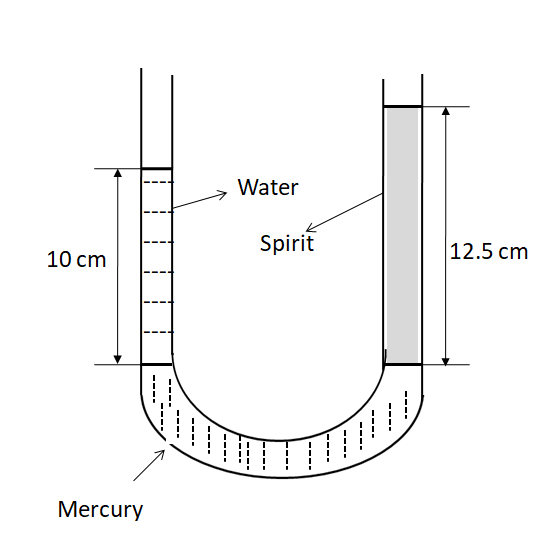
Solution
To answer this question, we need to use Pascal's law for the pressure in a fluid. Also, we need to know that the specific gravity of a liquid is its density with respect to the water.
Formula used:
⇒P=ρgh, where P is the pressure below a liquid column of height h and density ρ, and g is the acceleration due to gravity.
Complete step by step solution:
Let ρw and ρs be the respective densities of the water and the spirit.
Also, let h1 and h2 be the heights of the water and the spirit columns respectively.
We know from Pascal's law that inside a fluid, the pressure at the points which are at the same level is constant.
According to the question, the points A and B inside the U-tube in the below figure are at the same level. So the pressures at the points A and B are the same.
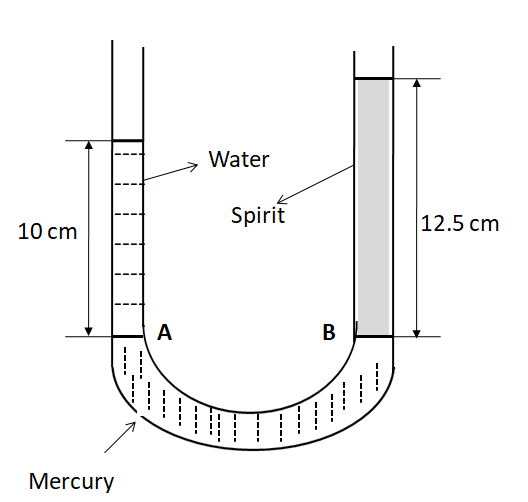
The pressure at the point A
⇒PA=Po+ρwgh1 …………………..(i)
And the pressure at the point B
⇒PB=Po+ρsgh2 ……………………….(ii)
(Here P0 is the atmospheric pressure)
By Pascal’s law
⇒PA=PB
From (i) and (ii), we have
⇒Po+ρwgh1=Po+ρsgh2
Cancelling P0 from both the sides, we get
⇒ρwgh1=ρsgh2
Dividing by g on both the sides
⇒ρwh1=ρsh2
⇒ρwρs=h2h1
According to the question, h1=10cm and h2=12.5cm
∴ρwρs=12.510
On solving, we get
⇒ρwρs=0.8 ……………………..(iii)
As we know that the specific gravity of a liquid is the ratio of its density to the density of water. So, the specific gravity of the spirit
⇒S=ρwρs
From (iii)
⇒S=0.8
Hence the specific gravity of the spirit is equal to 0.8.
Note:
While making the pressure balance using Pascal's law, we don’t need to convert all the quantities in the SI units. We just need to make sure that the respective quantities appearing in the equation must have the same units on both the sides.
