Question

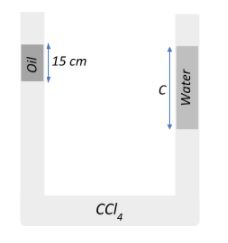
A ‘U’ tube contains oil, carbon tetrachloride and water as shown in the figure. The density of oil is $0.8\;gcm^{-3}$ and that of carbon tetrachloride is $1.6\;gcm^{-3}$. If oil and water surfaces are at the same level, find the height of the water column.

Answer 1

We know that hydrostatic pressure is a function of depth, but remains the same through all points at the same height. In this case, assume the water-$CCl_4$ interface as the height at which you measure the hydrostatic pressure. Consequently, the pressure at this height on the LHS column of the U-tube will also be the same. Equate the two pressures at this height in both columns to obtain a relation between our given fluid densities and the height of the oil, water and $CCl_4$ columns, and obtain the appropriate height of the water column.

Formula used:
Hydrostatic pressure $P = \rho gh$

Complete step-by-step answer:
We know that fluid (hydrostatic) pressure increases proportionally with depth because of the increasing weight of the fluid exerting a downward force. However, the pressure exerted by the fluid remains the same along every horizontal cross-section of the homogenous fluid, irrespective of the geometry of the vessel that holds the fluid. This can be attributed to the tendency of the fluid to achieve a state of equilibrium over its entire volume, even if the density distribution of the fluid is not uniform.
Now, the hydrostatic pressure of a fluid is given as:
$P = \rho gh$, where $\rho$ is the fluid density, g is the acceleration due to gravity, and h is the height of the fluid column.

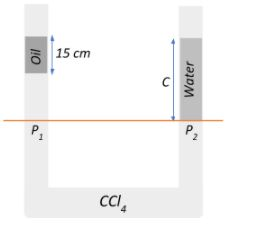
If we consider the horizontal line as shown in orange in the diagram, from our above discussion we know that the hydrostatic pressure will remain the same along this line since they are at the same height. Let us set out to calculate the hydrostatic pressure at this height in both the columns of the U-tube.
If $P_1$ is the hydrostatic pressure at that line on the LHS column of the U-tube and $P_2$ is the hydrostatic pressure at the line on the RHS column,
$P_1 = P_2$
Now, the LHS column at the horizontal line contains both oil and carbon tetrachloride, whereas the RHS column contains only water up until the horizontal line.
Given that the height of the oil column is $15\;cm$. Let the height of the water column be $C\;cm$, and thus the height of the $CCl_4$ column above the horizontal line will be $(C-15)\;cm$
$\Rightarrow \rho_{oil}g(15) + \rho_{CCl_4}g(C-15) = \rho_{water}g(C)$
$\Rightarrow \rho_{oil}(15) + \rho_{CCl_4}(C-15) = \rho_{water}(C)$
$\Rightarrow (0.8 \times 15) + (1.6 \times (C-15)) = C$
$\Rightarrow 12 -24 = C –1.6C$
$\Rightarrow 0.6C = 12 \Rightarrow C = \dfrac{12}{0.6} = 20\;cm$
Therefore, the height of the water column is found to be $20\;cm$

Note: Always remember that hydrostatic pressure exhibits a vertical pressure variation where the pressure is a function of the elevation. Also, all frictional and inertial stresses vanish, which is why the state of stress of the system is called hydrostatic. In this case, the entire fluid system exists in a state of equilibrium where points at the same height experience the same fluid pressure, even if the fluid is heterogeneous since the pressure gets distributed out evenly.