Question
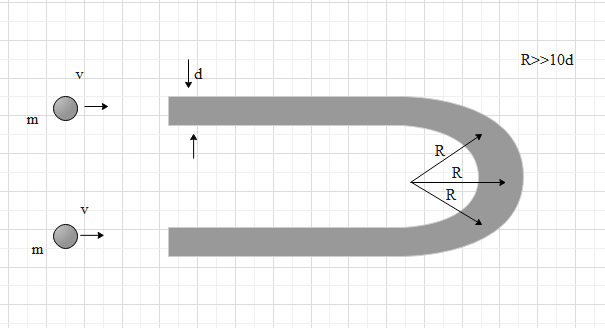
Question: A U-shaped tube of mass \(2\,m\) is placed on a horizontal surface. Two identical spheres each of di...
A U-shaped tube of mass 2m is placed on a horizontal surface. Two identical spheres each of diameter d( just less than the inner diameter of the tube) and mass m enter into the tube with velocity v as shown in the figure taking all conditions to be elastic and all surfaces are smooth. Find the following
(a) Speed of the tube where spheres are just about to collide inside the tube
(b) Speed of spheres where spheres are just about to collide
(c) Speed of spheres when they come out of the tube
(d) Speed of the tube when spheres come out
Solution
An elastic collision is a collision in which both the momentum and kinetic energy are conserved.
According to the law of conservation of momentum total initial momentum is equal to the total final momentum. Applying this conservation in the direction of initial velocity of balls we get
mv+mv=mv′+mv′+2mv′
Here, v’ is taken as the velocity of the tube when the spheres are just about to collide
According to the law of conservation of kinetic energy the total energy before collision and after collision will be equal.
21mv2+21mv2=21mv′′2+21mv′′2+212mv′2
Here, v” is the velocity of the sphere when they are about to collide.
Complete step by step answer:
An elastic collision is a collision in which both the momentum and kinetic energy are conserved.
Therefore, we can apply the conservation laws for momentum and kinetic energy for solving this question.
Given,
The mass of the ball is given as m.
The velocity of the ball is v.
U-shaped tube have mass 2m.
(a) According to the law of conservation of momentum total initial momentum is equal to the total final momentum. Applying this conservation in the direction of the initial velocity of balls we get,
mv+mv=mv′+mv′+2mv′
Here, v’ is taken as the velocity of the tube when the spheres are just about to collide.
On solving we get,
2mv=4mv′
⇒v′=2v
The speed of the tube where spheres are just about to collide inside the tube is 2v.
(b) According to the law of conservation of kinetic energy the total energy before the collision and after the collision will be equal.
Initially, the kinetic energy of balls is given as 21mv2
Let v” be the velocity of the sphere when they are about to collide.
Then, the kinetic energy of balls when they are about to collide is given as 21mv′′2.
The kinetic energy of tube when spheres are about to collide=212mv′2
Now, we can equate total energy before collision with total energy after collision
21mv2+21mv2=21mv′′2+21mv′′2+212mv′2
⇒mv2=mv′′2+mv′2 …………….…………..(1)
We have already found that,
v′=2v
Substitute this in equation (1)
Then we get,
mv2=mv′′2+mv′2
⇒mv2=mv′′2+m(2v)2
⇒mv2=mv′′2+4mv2
⇒mv2−4mv2=mv′′2
⇒v′′2=43v2
∴v′′=23v
Hence, Speed of the tube where spheres are just about to collide inside the tube= 2v.
The speed of spheres where spheres are just about to collide is 23v.
(c) Initially the two balls together had a total momentum of 2mv, and the tube had zero momentum. Finally, after the collision, the momentum of the balls is transferred to the tube.
So, the speed of spheres, when they come out of the tube, is zero.
(d) Since the mass of the tube is 2m. To conserve momentum the tube should move with a velocity v after the collision so that final momentum remains 2mv.
The speed of the tube when spheres come out is v.
Note:
Here it is given that the tube is initially at rest. Hence the initial velocity of the tube is zero. Therefore, the initial momentum will be the sum of the momentum of two balls only. If the tube was already in motion before the balls entered the tube then we should also add the momentum of the tube while calculating total initial momentum.
Initially, the two balls together had a total momentum of 2mv, and the tube had 0 momentum. Finally, after collision, the momentum of the balls is transferred to the tube. Since the mass of the tube is 2m, to conserve momentum the tube should move with a velocity v. After the collision and the balls come to rest.
