Question

A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is ${60^0}$. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is ${30^0}$. Find the height of the tower and the width of the canal.

Answer 1

First draw the diagram accurately according to the question given, it is a must for height and distance related problems. Then consider two triangles one with ${60^0}$ angle and other with ${30^0}$ angle. Assume the width of the canal as x and height of tower as h. Then apply suitable trigonometry ratios in both the triangles. Solve these two using suitable algebraic computations to find the value of two needed values.

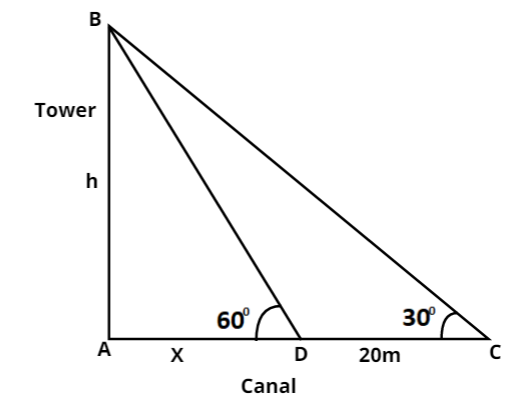
Complete step-by-step answer:
Let us consider the diagram given above. Let us assume that the height of the tower is h meters and the width of the canal is x meters.
So, we have from the diagram,
AB = h
AD = x
CD = 20
$\angle BCA = {30^0}$
$\angle BDA = {60^0}$
In $\vartriangle ABC$, we have Tangent value is the ratio of perpendicular to base, so
$\tan {30^0} = \dfrac{{AB}}{{AC}} \\\ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + 20}} \\\$( As we know that value of $\tan {30^0} = \dfrac{1}{{\sqrt 3 }}$ )
Simplifying the above equation, we get
$\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + 20}}....(1)$
Now, In $\vartriangle ABD$, we have Tangent value is the ratio of perpendicular to base, so
$\tan {60^0} = \dfrac{{AB}}{{AD}} \\\ \Rightarrow \sqrt 3 = \dfrac{h}{x} \\\ \Rightarrow x = \dfrac{h}{{\sqrt 3 }}...(2) \\\$( As we know that value of $\tan {60^0} = \sqrt 3$ )
From equation (2), we can substitute the value of x in equation (1), to get the following expression
$\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{\dfrac{h}{{\sqrt 3 }} + 20}}$
Now let us do the cross multiplication in above equation, we get
$h\sqrt 3 = \dfrac{h}{{\sqrt 3 }} + 20$
Multiply the above equation by $\sqrt 3$ on both LHS and RHS. Then we get,

$$3h = h + 20\sqrt 3 \\\ \Rightarrow h = 10\sqrt 3 \\\$$

Substitute this value of h in equation (2),
$x = \dfrac{{10\sqrt 3 }}{{\sqrt 3 }} \\\ \Rightarrow x = 10 \\\$

$\therefore$ The height of the tower is $10\sqrt 3$ meters. And the width of the canal is 10 meters.

Note: The above problem is a very popular kind of height and distance problem. In such cases proper visualization of the question with proper diagrams is must. Angle of elevation and angle of depression both will be the same for the given pair of objects. Utilization of the trigonometry ratios and their values according to the terms given of sides and angles is must. Some algebraic simplification will definitely make the process easy to get the correct solution.