Question

A TV tower has a height of 75 m. The maximum distance and area up to which this TV transmission can be received is
(Radius of the Earth = 6400 km)
A) $31km,3018k{m^2}$
B) $30km,3000k{m^2}$
C) $28km,2800k{m^2}$
D) $25km,2500k{m^2}$

Answer 1

In this question, we need to determine the maximum distance and area up to which this TV transmission can be received. For this we will use the concept that the maximum distance and area up to which this TV transmission is the range of the transmission up to which a signal can be received.

Complete step by step answer:

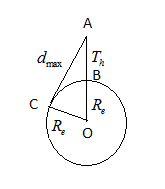
Height of the tower ${T_h} = 75m = 0.075km$
Radius of the Earth${R_e} = 6400km$
We know towers are situated vertically above the earth surface and they transmits signals in equal distance, in the figure $\angle ACO = {90^ \circ }$
Let AC be the maximum distance in which signal can be transmitted, OC is the radius of the earth ${R_e}$and AB is the sum of the radius of earth and height of the tower
Also when a signal reaches the earth surface they are tangent to the earth surface hence we can say$\angle ACO = {90^ \circ }$, so by using the Pythagoras theorem $\vartriangle ACO$we can write

$$A{0^2} = A{C^2} + C{O^2} \\\ {\left( {AB + BO} \right)^2} = A{C^2} + C{O^2} \\\ {\left( {{T_h} + {R_e}} \right)^2} = {\left( {{d_{\max }}} \right)^2} + R_e^2 \\\ T_{_h}^2 + R_e^2 + 2{T_h}{R_e} = {\left( {{d_{\max }}} \right)^2} + R_e^2 \\\ {\left( {{d_{\max }}} \right)^2} = T_{_h}^2 + 2{T_h}{R_e} \\\ {d_{\max }} = \sqrt {T_{_h}^2 + 2{T_h}{R_e}} - - - (i) \\\$$

Since the height of the tower${T_h} \ll {R_e}$, hence we can write equation (i) as
${d_{\max }} = \sqrt {2{T_h}{R_e}} - - (ii)$
Now substitute the value of ${T_h} = 0.075km$and ${R_e} = 6400km$in equation (ii) we get

$${d_{\max }} = \sqrt {2\left( {0.075} \right)\left( {6400} \right)} \\\ = \sqrt {960} \\\ = 30.98 \\\ = 31km \\\$$

Hence the maximum distance which this TV transmission can be received is $= 31km$
Now calculate for the area of the range of transmission, since the transmission from the tower cover the same range of length all-round the tower hence the area of transmission will be in a circle, where area of the circle is$A = \pi {r^2}$, hence area of transmission will be

$$A = \pi \times 31 \times 31 \\\ = 3.14 \times 31 \times 31 \\\ = 3018k{m^2} \\\$$

Hence area up to which this TV transmission can be received$= 3018k{m^2}$
Option A is correct.

Note: A transmission is the process of sending and propagating a signal using a wired, optical or wireless electromagnetic transmission. Students must note that the range of signal from a tower which it covers when it is viewed from the top makes a circle.