Question
Question: A turn of radius \(20m\) is banked for the vehicles going at a speed of \(36km/h\). If the coefficie...
A turn of radius 20m is banked for the vehicles going at a speed of 36km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
A) 14.7km/h and 54km/h
B) 14.2km/h and 50km/h
C) 11.7km/h and 44km/h
D) 17.7km/h and 34km/h
Solution
In this question we want to find the range of speed of vehicle so that it neither slip down nor skids up
We take two possible conditions when a vehicle moving its maximum speed means if it increases its speed now it will skid up. In this condition we mark all forces and balance them and same thing we will do for minimum speed friction gives required centripetal force for turn
Complete step by step answer:
In the question it is given radius of turn r=20m and banked with angle θ for speed v=36km/h=1836×5=10m/sec
And coefficient of friction μ=0.4
From here we can find the value of tanθ
We know tanθ=rgv2
⇒tanθ=20×10102=21 .............. (1)
We assume two conditions one when a vehicle moves with maximum speed in this condition the vehicle may skid up if speed will increase.
In this situation friction between road and tyre is opposite to skidding direction as shown in figure
We mark all forces on vehicle as shown in figure and dividing them in their component
From figure clearly see that if vehicle is in equilibrium so the force acting on vehicle are equal along the road and perpendicular to the road
Force along the road
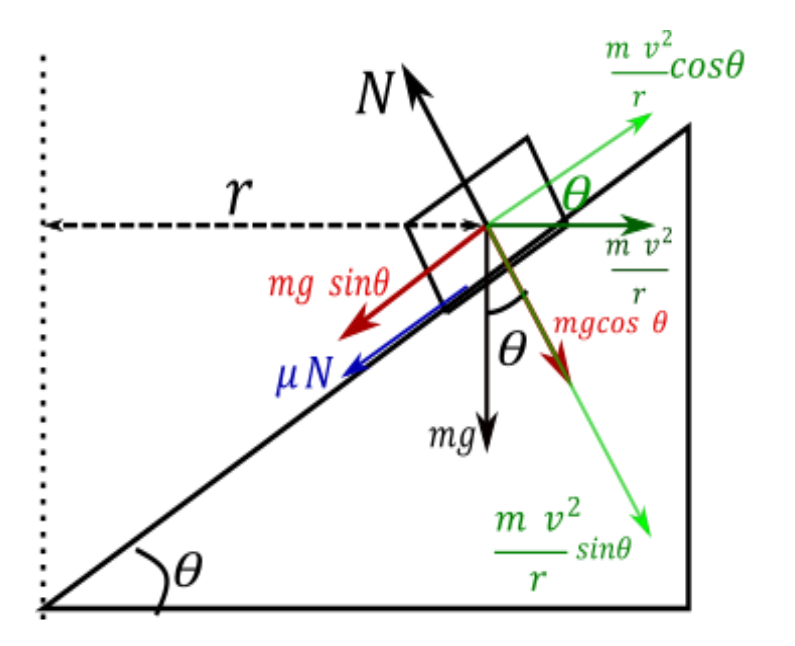
⇒mgsinθ+μN=rmv2cosθ
Rearranging this equation
⇒μN=rmv2cosθ−mgsinθ ............ (2)
Now take forces perpendicular to road
⇒N=mgcosθ+rmv2sinθ ............... (3)
Divide (2) by (3)
⇒μ=mgcosθ+rmv2sinθrmv2cosθ−mgsinθ
Solving this equation we get
⇒μ=rgcosθ+v2sinθv2cosθ−rsinθ
Right hand side divided by cosθ
⇒μ(rg+v2tanθ)=v2−rgtanθ
Solving this we can find value of v maximum velocity of vehicle where it will not skid
⇒v=1−μtanθrgtanθ+μrg
Put the given values in this equation
⇒v=1−0.4×2120×10×21+0.4×20×10
⇒v=225
v=15m/sec
Convert into km/h
Maximum speed v=54km/h
Now we take the minimum speed case in this case friction applied in upward direction along the road as shown in figure.
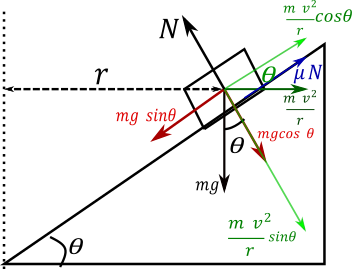
Equate Forces along road
⇒μN+rmv2cosθ=mgsinθ
⇒μN=mgsinθ−rmv2cosθ .................. (4)
Forces perpendicular to road
⇒N=mgcosθ+rmv2sinθ ............... (5)
Divide (4) by (5)
⇒μ=mgcosθ+rmv2sinθmgsinθ−rmv2cosθ
Solving this we get
⇒μ=rgcosθ+v2sinθrgsinθ−v2cosθ
Divide right hand side by cosθ
⇒μ=rg+v2tanθrgtanθ−v2
Further solving it we get
⇒v=μtanθ+1rgtanθ−μrg
Putting given values in above equation
⇒v=0.4×21+120×10×21−0.4×20×10
By solving this
⇒v=16.66
Minimum speed
∴v=4.08m/sec
Convert into km/h
v=4.08×518=14.68km/h
Hence the minimum speed is 14.7km/h
Hence in this question option A is correct
Note: We get the range of speed of vehicle is 14.7km/h to 54km/h its means that if vehicle moves with slower speed then 14.7km/h than it will slip down because friction in upward direction can not provide sufficient centripetal force to take turn
And if a vehicle moving with higher speed then 54km/h then the friction force can not provide centripetal force to hold the vehicle so it will skid up.
