Question

A tunnel through a mountain for a four-lane highway is to have an elliptical opening. The total width of the highway is to be $16m$, and the height at the edge of the road must be sufficient for a truck $4m$ high to clear the highest point of the opening is to be $5m$ approximately. How wide must the opening be?

Answer 1

The width of the opening will be wider than the width inside the tunnel. We are going to use the advantage of the elliptical shape of the opening. Draw the layout of the opening and mark the coordinates and find out the unknown values.

Complete step-by-step answer:
As per the information provided,
A tunnel through a mountain for a four-lane highway is to have an elliptical opening.
The total width of the highway is to be $16m$, which is on the inside. So, at opening it must be wider than this.
One more condition they have given that,
The height at the edge of the road must be sufficient for a truck $4m$ high to clear the highest point of the opening is to be $5m$ approximately.
So, this $5m$ will be the total height which is the semi minor axis of the ellipse.
Let us consider the width of the tunnel at the opening is $2a$ as it resembles the length of the major axis.
You will get clear clarity when you analyze the following diagram where I have located all the above-mentioned points.

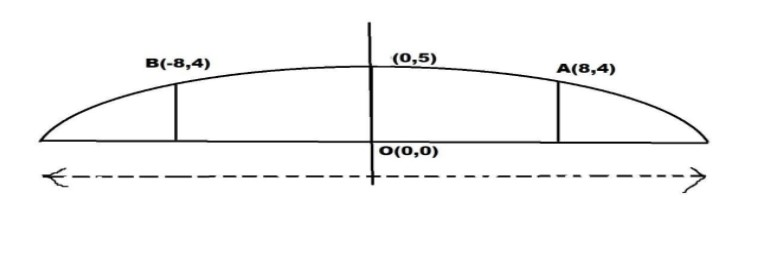
From the diagram, we can conclude that the opening is in the shape of an ellipse.
So, the general formula of the ellipse is $\left( {\dfrac{{{x^2}}}{{{a^2}}}} \right) + \left( {\dfrac{{{y^2}}}{{{b^2}}}} \right) = 1$
Where $2a$ is the length of major axis and $2b$ is length of the minor axis where $b$ value is $5$ because of the given condition in the question.
From the diagram we can say that point $A\left( {8,4} \right)$ lies on the ellipse.
So, substitute those values in the equation of the ellipse, we will get
$\Rightarrow \left( {\dfrac{{{8^2}}}{{{a^2}}}} \right) + \left( {\dfrac{{{4^2}}}{{{5^2}}}} \right) = 1$
So, simplify the above equation to get the $a$ value
$\Rightarrow \left( {\dfrac{{{8^2}}}{{{a^2}}}} \right) = 1 - \left( {\dfrac{{16}}{{25}}} \right) \\\ \Rightarrow \left( {\dfrac{{{8^2}}}{{{a^2}}}} \right) = \dfrac{{25 - 16}}{{25}} \\\ \Rightarrow \left( {\dfrac{{{8^2}}}{{{a^2}}}} \right) = \dfrac{9}{{25}} \\\ \Rightarrow {\left( {\dfrac{8}{a}} \right)^2} = {\left( {\dfrac{3}{5}} \right)^2} \\\$
Applying square root on both sides, we will get
$\Rightarrow \left( {\dfrac{8}{a}} \right) = \left( {\dfrac{3}{5}} \right) \\\ \Rightarrow a = \dfrac{{8 \times 5}}{3} \\\ \Rightarrow a = \dfrac{{40}}{3} \\\ \Rightarrow a = 13.33 \\\$
So, the value of $a$ is $13.33$ but we need the value of $a$ which is equal to the width of the tunnel at the opening.
Hence, the width of tunnel at the opening $= 2a$
$= 2 \times 13.33 \\\ = 26.66 \\\$
So, the required the width of tunnel at the opening is $26.6m$.

Note: Imagine the situation and draw the diagram accordingly. Then after you can substitute any value point that lies on the locus to find the unknowns.Students should remember the general equation of ellipse i.e $\left( {\dfrac{{{x^2}}}{{{a^2}}}} \right) + \left( {\dfrac{{{y^2}}}{{{b^2}}}} \right) = 1$ to solve these types of questions.