Question
Question: A tunnel is dug along the diameter of the earth (radius R and mass M). There is a particle of mass ‘...
A tunnel is dug along the diameter of the earth (radius R and mass M). There is a particle of mass ‘m’ at the center of the tunnel. Find the minimum velocity given to the particle so that it just reaches to the surface of the earth is-
A. RGM
B. 2RGM
C. R2GM
D. It will reach with the help of a negligible velocity
Solution
First, we will apply the concept of conservation of energy and then find out the values of initial kinetic energy, initial potential energy, final kinetic energy and final potential energy respectively to get the required answer. Refer to the solution below.
Complete answer:
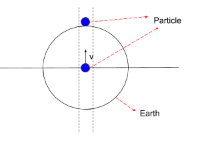
We will simply use the concept of conservation of energy which states that the initial total energy is equal to the final total energy-
⇒TEi=TEf
Now, it is clear that the initial total energy is the sum of initial kinetic energy and initial potential energy. Similarly, final total energy is the sum of final kinetic energy and final potential energy-
⇒KEi+PEi=KEf+PEf
Let this equation be equation 1.
⇒KEi+PEi=KEf+PEf (equation 1)
We should already know that if there is a solid sphere and inside it is a particle of mass m which is at r distance from the center, then its gravitational potential energy is calculated by-
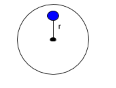
⇒GPE=R3−GMm(23R2−2r2)
Where, M is the mass of the planet, R is the radius of the planet and r is the distance between the particle and the center of the planet.
When the particle is on the surface of the planet, the gravitational potential energy is calculated by-
⇒GPE=R−GMm
Where, M is the mass of the planet, m is the mass of the particle and R is the radius of the planet.
Initially, the velocity provided to the particle is v with mass m. Hence, initial kinetic energy will be-
⇒KEi=21mv2
Let this equation be equation 2.
⇒KEi=21mv2 (equation 2)
The particle is initially at the center of the Earth. Hence, the distance of the particle from the center (r) will be zero. The formula applied will be-
⇒GPE=R3−GMm(23R2−2r2) (since the particle is inside the Earth)
Therefore, initial potential energy will be-
⇒PEi=R3−GMm(23R2−202) (since the value of r is zero)
Let this equation be equation 3.
⇒PEi=R3−GMm(23R2) (equation 3)
Since it is asked in the question that the particle should just reach the surface of the earth and no further then it means that the final kinetic energy will be zero-
⇒KEf=0
Let the above equation be equation 4.
⇒KEf=0 (equation 4)
Since the particle is on the surface of the Earth, the formula used to calculate its potential energy will be-
⇒GPE=R−GMm
Therefore, final potential energy will be-
(Since the radius of the earth is given as R. The distance between the particle and the surface of the earth will be negligible as compared to the radius of the Earth. Hence, the distance between the particle and the center of the Earth will also be R)
⇒PEf=R−GMm
Let this equation be equation 5.
⇒PEf=R−GMm (equation 5)
Now, substituting the values of equation 2, equation 3, equation 4 and equation 5 into equation 1, we will get-
⇒KEi+PEi=KEf+PEf ⇒21mv2+[R3−GMm(23R2)]=0+(R−GMm) ⇒21mv2−R3GMm(23R2)=R−GMm ⇒21mv2=R−GMm+R3GMm×(23R2) ⇒21mv2=R−GMm+RGMm×23 ⇒21mv2=RGMm(23−1) ⇒21mv2=RGMm×21 ⇒v2=RGM ⇒v=RGM
So, the correct answer is “Option A”.
Note:
The energy conservation law states that energy cannot be created or destroyed. It can always be converted from one form to another, however. The total energy of an individual system remains constant, if you consider all types of energy. All sources of energy are subject to the law of energy conservation.
