Question

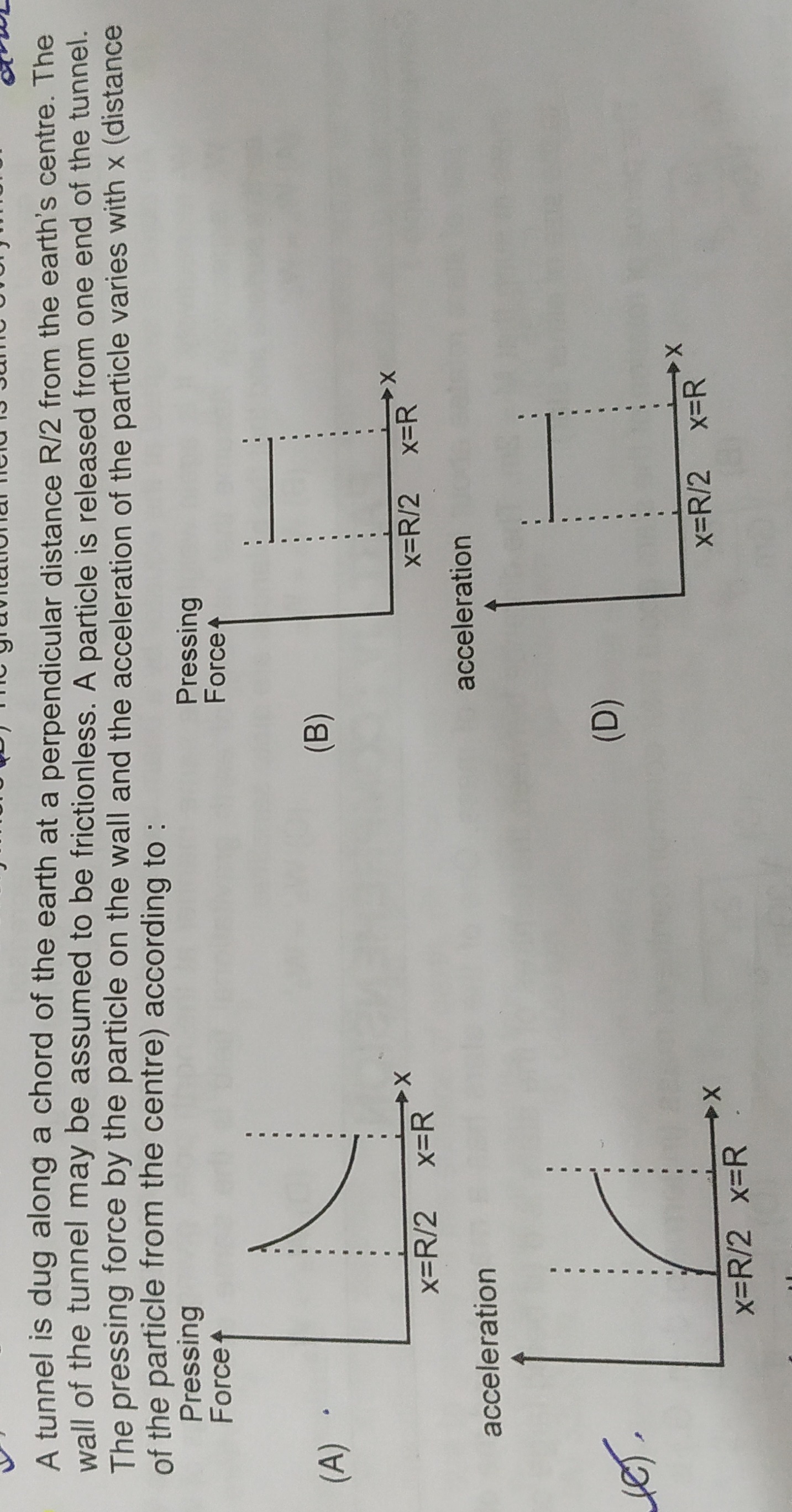
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall and the acceleration of the particle varies with x (distance of the particle from the centre) according to :

Answer 1

B, C

Answer 2

The problem asks us to determine how the pressing force by the particle on the wall and the acceleration of the particle vary with its distance 'x' from the Earth's center, as it moves through a frictionless tunnel dug along a chord. The tunnel is at a perpendicular distance $d = R/2$ from the Earth's center.

1. Gravitational Force Inside the Earth:

For a particle of mass 'm' at a distance 'x' from the center of a uniformly dense Earth, the gravitational acceleration $g'$ is given by: $g' = \frac{gx}{R}$

The gravitational force acting on the particle is $F_g = mg' = \frac{mgx}{R}$. This force is always directed towards the center of the Earth.

2. Geometry of the Tunnel:

Let the origin be at the Earth's center. The tunnel is a chord at a perpendicular distance $d = R/2$ from the center. Let 'y' be the distance of the particle from the midpoint of the chord. The distance 'x' from the particle to the Earth's center is related by the Pythagorean theorem: $x^2 = d^2 + y^2$

Since $d = R/2$, we have $x^2 = (R/2)^2 + y^2$.

The particle is released from one end of the tunnel. The ends of the chord lie on the surface of the Earth, meaning $x_{max} = R$.

At the midpoint of the chord, $y=0$, which gives $x_{min} = d = R/2$.

So, the distance 'x' of the particle from the Earth's center varies from $R/2$ to $R$.

3. Pressing Force (Normal Force):

The gravitational force $F_g = \frac{mgx}{R}$ acts towards the Earth's center. We need to resolve this force into components parallel and perpendicular to the tunnel.

Let $\theta$ be the angle between the position vector of the particle (from the Earth's center) and the line perpendicular to the chord (passing through the Earth's center and the midpoint of the chord).

From the geometry, $\cos\theta = \frac{d}{x}$.

The component of the gravitational force perpendicular to the tunnel is $F_{\perp} = F_g \cos\theta$.

The pressing force (normal force) $N$ exerted by the wall on the particle balances this perpendicular component: $N = F_{\perp} = \left(\frac{mgx}{R}\right) \left(\frac{d}{x}\right) = \frac{mgd}{R}$

Substitute $d = R/2$: $N = \frac{mg(R/2)}{R} = \frac{mg}{2}$

Since 'm', 'g', and 'R' are constants, the pressing force $N$ is constant throughout the particle's motion in the tunnel.

Looking at the graphs:

• Graph (A) shows a varying pressing force, which is incorrect.
• Graph (B) shows a constant pressing force between $x=R/2$ and $x=R$. This matches our derivation.

4. Acceleration of the Particle:

The net force causing the particle's acceleration along the tunnel is the component of $F_g$ parallel to the tunnel.

From the geometry, $\sin\theta = \frac{y}{x}$.

The component of gravitational force along the tunnel is $F_{||} = F_g \sin\theta$.

According to Newton's second law, $ma = F_{||}$: $ma = \left(\frac{mgx}{R}\right) \left(\frac{y}{x}\right) = \frac{mgy}{R}$

So, the acceleration of the particle is $a = \frac{gy}{R}$.

This acceleration is directed towards the midpoint of the chord.

To express 'a' as a function of 'x', we use the relation $y = \sqrt{x^2 - d^2}$.

Substituting $d=R/2$: $y = \sqrt{x^2 - (R/2)^2}$

Therefore, $a = \frac{g}{R} \sqrt{x^2 - (R/2)^2}$.

Let's analyze this function:

• At $x = R/2$ (midpoint of the chord, $y=0$), $a = \frac{g}{R} \sqrt{(R/2)^2 - (R/2)^2} = 0$.
• At $x = R$ (end of the tunnel, $y = \sqrt{R^2 - (R/2)^2} = \sqrt{3R^2/4} = \frac{\sqrt{3}}{2}R$), $a = \frac{g}{R} \left(\frac{\sqrt{3}}{2}R\right) = \frac{\sqrt{3}}{2}g$.

The function $a(x) = \frac{g}{R} \sqrt{x^2 - (R/2)^2}$ is an increasing function of 'x' for $x \ge R/2$.

To determine the shape, we can look at the second derivative. $a'(x) = \frac{g}{R} \frac{x}{\sqrt{x^2 - (R/2)^2}}$ (positive, so increasing)

$a''(x) = \frac{g}{R} \frac{\sqrt{x^2 - (R/2)^2} - x \frac{x}{\sqrt{x^2 - (R/2)^2}}}{x^2 - (R/2)^2} = \frac{g}{R} \frac{(x^2 - (R/2)^2) - x^2}{(x^2 - (R/2)^2)^{3/2}} = \frac{g}{R} \frac{-(R/2)^2}{(x^2 - (R/2)^2)^{3/2}}$

Since $a''(x)$ is negative, the curve is concave down.

Looking at the graphs:

• Graph (C) shows acceleration starting from 0 at $x=R/2$ and increasing to a maximum value at $x=R$, with a concave down shape. This matches our derivation.
• Graph (D) shows a constant acceleration, which is incorrect.

Conclusion:

The pressing force is constant, as shown in graph (B).

The acceleration varies as $a = \frac{g}{R} \sqrt{x^2 - (R/2)^2}$, which is an increasing function of 'x' and concave down, as shown in graph (C).

The question asks for the variation of both quantities. Therefore, both graphs (B) and (C) are correct representations.