Question

A tuning fork of frequency 340HZ is sounded above a cylindrical tube 1m long. Water is slowly poured into the tube. If the speed of sound is $340m{s^{ - 1}},$ at what levels of water in the tube will the sound of the tuning fork be appreciably intensified?
(A). 25cm, 75cm
(B). 20cm, 80cm
(C). 23cm, 67cm
(D). 40cm, 80cm

Answer 1

The sound of tuning fork tends to get intensified at the resonance. Firstly we will calculate the resonance of the tuning fork and then we will find the levels of the water in the tube when the sound of the tuning fork will be appreciably intensified.

Complete step by step solution:
Given that the frequency of the tuning fork is 340HZ and the speed of the sound of the tuning fork is 340m/s.
The following diagram gives a visual representation of the given question scenario perfectly:

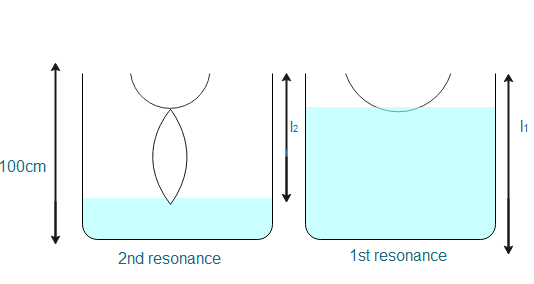
Since the sound of the tuning fork is intensified at resonance.
For first resonance
The length is given by ${l_1} = \dfrac{\lambda }{4}$
Where ‘$\lambda$’ represents the wavelength of wave.
$\Rightarrow {l_1} = \dfrac{\gamma }{f} \times \dfrac{1}{4}$
We know that, v=340m/s, f = 340HZ, so substituting these values in the above equation we get:
\eqalign{ & {l_1} = \dfrac{{340}}{{340}} \times \dfrac{1}{4} \cr & \Rightarrow {l_1} = \dfrac{1}{4} \cr & \therefore {l_1} = 0.25m = 25cm \cr}
Now for the second resonance, the length is will given by
\eqalign{ & {l_2} = \dfrac{{3\lambda }}{4} \cr & \Rightarrow {l_2} = \dfrac{{3v}}{f} \times \dfrac{1}{4} \cr}
Again substituting the known values in the above equation, i.e. v=340m/s, f = 340HZ. So, we get:
\eqalign{ & {l_2} = \dfrac{3}{4} \times \dfrac{{340}}{{340}} \cr & \Rightarrow {l_2} = \dfrac{3}{4} \cr & \therefore {l_2} = 0.75m = 75cm \cr}
We have to calculate the levels of water for both cases. That can be obtained by subtracting the two calculated lengths from 100. So mathematically, we have:
$100 - {l_1} = 100 - 25cm = 75cm$
And $100 - {l_2} = 100 - 75cm = 25cm$
Therefore, the levels of water are 75cm and 25cm when the sound of the tuning fork is intensified.

Therefore the correct option is (A).

Note:
A tuning fork serves as a useful illustration of how a vibrating object can produce sound. When the tuning fork is hit with a rubber hammer, it begins to vibrate to calculate the levels of water, we need to calculate the length for two cases of resonance.