Question

A tuning fork of frequency $328{\text{ }}Hz$ is moved towards a wall at a speed of $2m/s$ . An observer standing on the same side as the fork hears two sounds, one directly from the fork and the other reflected from the wall. No. of beats per second is:
(Velocity of sound in air $330m/s$ ).
A. 4
B. 5
C. 6
D. 7

Answer 1

Hint This question can be solved using Doppler effect. When the source is moving towards the observer there is a change in frequency. This changed frequency and frequency reflected from the wall will produce beats. As we know the difference of frequency is called beats.

Complete step-by-step solution :When a sound object moves towards you, the frequency of the sound waves increases, leading to a higher pitch. Conversely, if it moves away from you, the frequency of the sound waves decreases and the pitch comes down. The drop-in pitch of ambulance sirens as they pass by and the shift in red light are the result of the Doppler effect.

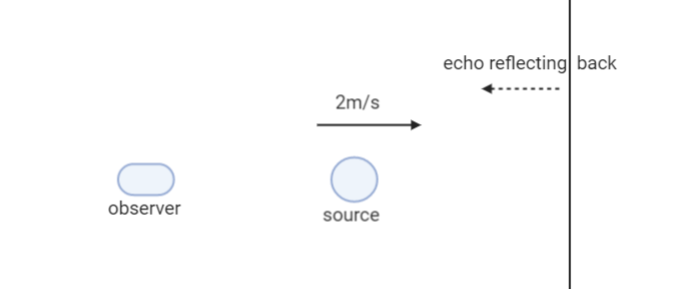
Frequency when source is receding observer.
$f' = f\dfrac{v}{{v + {v_s}}}$
$f = 328$
$v = 330$
${v_s} = 2$
${f_1}' = 328(\dfrac{{330}}{{330 + 2}}) = 328(\dfrac{{330}}{{332}})$
Frequency when source is approaching observer i.e. frequency of echo:
$f' = f\dfrac{v}{{v - {v_s}}}$
${f_2}' = 328(\dfrac{{330}}{{330 - 2}}) = 328(\dfrac{{330}}{{328}})$
Now, calculating the number of beats: which is the absolute difference of two frequencies.
$|{f_1}' - {f_2}'| = |328(\dfrac{{330}}{{332}}) - 328(\dfrac{{330}}{{328}})|$
$|{f_1}' - {f_2}'| = 330(328)(\dfrac{4}{{328 \times 332}}) = 4$
Hence, option A is correct.

Note:- The Doppler Effect can also be used in astronomy in relation to light waves depending on the fact that the spectra of stars are not constant. As absorption lines exhibited by different stars are different at defined frequencies, but the Doppler Effect is identifiable only when these absorption lines are away from these defined frequencies.