Question

A tube of length $L$ if filed with an incompressible liquid of mass $M$ and closed at both ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity $\omega$. The force exerted by the liquid at the other end will be
A. $\dfrac{1}{2}{M^2}{\omega ^2}L$
B. $\dfrac{1}{2}M{\omega ^2}L$
C. $\dfrac{1}{2}M{\omega ^2}{L^2}$
D. None of the above

Answer 1

In order to solve this question you have to remember that the force exerted by liquid at the other end is due to the centripetal force because of rotation. You have to take a small strip of that tube and then find force on that and then integrate that for the whole tube of length $L$ to find the total force on the tube.

Complete step by step solution:

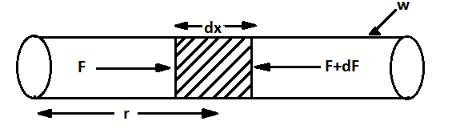
Let the length of a small element of tube be $dx$
And the mass of this small element is given by,
$dm = \dfrac{M}{L}dx$
Where, $M$ is the mass of filled liquid and the given length of the tube is $L$ .
The the force on that element is given by,
$dF = dm \times x{\omega ^2}$
On integrating both sides, we have
$\int\limits_0^F {dF} = \dfrac{M}{L}{\omega ^2}\int\limits_0^L {xdx}$
On further solving and putting the limits we have,
$\Rightarrow F = \dfrac{M}{L}{\omega ^2}\left[ {\dfrac{{{L^2}}}{2}} \right]$
On further simplification, we have
$\Rightarrow F = \dfrac{1}{2}M{\omega ^2}L$
Hence, the force exerted by the liquid at the other end is given by $\dfrac{1}{2}M{\omega ^2}L$

Therefore, the correct option is (B)

Note: A centripetal force is defined as force which compels a body to travel in a closed curved path. Its direction is perpendicular to the motion of the body and toward a certain fixed point of the instantaneous centre of curvature of the path. One common example for centripetal force is the case in which a body moves with uniform speed along a circular path. The centripetal force is perpendicular to the direction of the motion and also along the radius towards the centre of the circular path. Centripetal force only causes a change in velocity and not speed.