Question

A tube of air 2 feet in length has a pressure versus distance graph as shown at $t = 0$. It is vibrating in one of its allowed standing wave modes. Which standing wave is this?
A. Fundamental
B. Second harmonic
C. Second overtone
D. First overtone

Answer 1

Standing waves are stationary waves, which are a combination of two waves moving in opposite directions with the same amplitude and frequency. Use the concept of frequency of vibration.

Complete answer:
We have different types of pipes to study. Both closed ended, both open ended, one closed and one open ended. In this particular question, we observe that the pipe is closed from the left end and open from the right end. We also know that the closed end side develops high pressure and the open end side develops low pressure. This also can be observed in the given diagram, In this case, at the left end a displacement node and at the right end, an antinode is formed.

The frequency of vibration for this mode is given by,
$f = \dfrac{v}{\lambda }$
Where, f is frequency of vibration, $\lambda$ is wavelength of this node of vibration, v is the velocity of sound in the air.

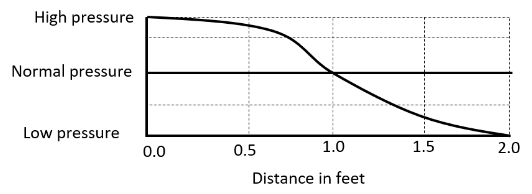
In the above diagram, we can observe that the given formula would yield the lowest value of frequency because there is only one node and antinode for both pressure and displacement. The wavelength in this mode is four times the length of the pipe. Therefore, we can express the frequency of the wave as,
$f = \dfrac{v}{{4l}}$, where, l is the length of the tube.

We know that the fundamental frequency that is the lowest frequency of vibration is given as,
$f = \dfrac{v}{{4l}}$
Therefore, the standing wave represents the fundamental frequency of vibration.

So, the correct answer is option A.

Note: When the two waves of the same magnitude propagate in the opposite direction, their resultant wave is known as standing wave. In the standing waves, the nodes appear at the integer multiple of$\dfrac{\lambda }{2}$ and the antinode appears at odd multiples of $\dfrac{\lambda }{4}$. Students should memorize that the Second harmonic has two times the fundamental frequency.