Solveeit Logo
Login

Question

Question: A tube is mounted so that it’s base is at height \('h'\)above the horizontal ground. The tank is fil...

A tube is mounted so that it’s base is at height ′h′'h'above the horizontal ground. The tank is filled with water to a depth hh. A hole is punched in the side of the tank at depth yy below the water surface. Then the value of yy so that the range of the emerging stream would be maximum?
A. hh

B. h2\dfrac{h}{2}

C.h4\dfrac{h}{4}

D. 3h4\dfrac{3h}{4}

Explanation

Solution

Draw proper diagram. Convert word problems into equations and use the equation of laws of motion to solve it.
Formula used: s=ut+12a+2s = ut + \dfrac{1}{2}a + 2
v2=u2=2as{v^2} = {u^2} = 2as

Complete step by step answer:


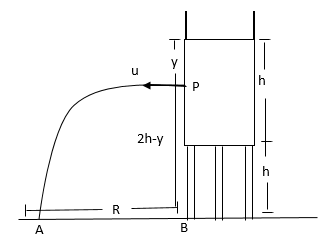
Let a tube be mounted at height hhfrom the ground.
Then, it is filled by water to a height, hh.
Then , a hole is punched in the side of the tank at depth yybelow the water surface.
Let the water coming out of the hole fall in the form of stream at point A.A.
Then distance ABABis the range R.R.
Let PPbe the point where the hole is punched.
⇒PB=2h−y\Rightarrow PB = 2h - y
From the Newton’s laws of motion,
We know that
s=ut+12at2s = ut + \dfrac{1}{2}a{t^2}
⇒2h−y=0+12gt2\Rightarrow 2h - y = 0 + \dfrac{1}{2}g{t^2}
Vertical velocity is zero in case of horizontal projectile.
Rearranging the equation, we get
t2=2(2h−y)g{t^2} = \dfrac{{2\left( {2h - y} \right)}}{g}
t=2(2h−y)gt = \sqrt {\dfrac{{2\left( {2h - y} \right)}}{g}}
Now, since range is the horizontal distance, and distance=speed×time = speed \times time
We can write,
R=u×tR = u \times t . . . . . (1)
Now, we know that
v2=u2=2as{v^2} = {u^2} = 2as
For horizontal velocity of projectile final velocity is zero.
⇒−u2=2as\Rightarrow - {u^2} = 2as
Also, a=ga = gand s=−ys = - y
⇒−u2=2g(−y)\Rightarrow - {u^2} = 2g\left( { - y} \right)
⇒u2=2gy\Rightarrow {u^2} = 2gy
⇒u=2gy\Rightarrow u = \sqrt {2gy}
Put the value of uuand ttin equation (1) to calculate R.R.
⇒R=2gy×2(2h−y)g\Rightarrow R = \sqrt {2gy} \times \sqrt {\dfrac{{2\left( {2h - y} \right)}}{g}}
Multiplying, we get
R=2gy(2h−y)gR = 2\sqrt {\dfrac{{gy\left( {2h - y} \right)}}{g}}
⇒R=2y(2h−y)\Rightarrow R = 2\sqrt {y\left( {2h - y} \right)}
Now, RRis maximum if
dRdy=0\dfrac{{dR}}{{dy}} = 0 and (d2Rdy2)<0\left( {\dfrac{{{d^2}R}}{{d{y^2}}}} \right) < 0
⇒dRdy=ddy[2y(2h−y)]\Rightarrow \dfrac{{dR}}{{dy}} = \dfrac{d}{{dy}}\left[ {2\sqrt {y(2h - y)} } \right]
=2ddy2hy−y2= 2\dfrac{d}{{dy}}\sqrt {2hy - {y^2}}
=212hy−y2ddy(2hy−y2)= 2\dfrac{1}{{\sqrt {2hy - {y^2}} }}\dfrac{d}{{dy}}\left( {2hy - {y^2}} \right)
(∵ddxxn=nxn−1)\left( {\because \dfrac{d}{{dx}}{x^n} = n{x^{n - 1}}} \right)
=22hy−y2×(2h−2y)= \dfrac{2}{{\sqrt {2hy - {y^2}} }} \times \left( {2h - 2y} \right)
∴dRdy=0\therefore \dfrac{{dR}}{{dy}} = 0
⇒22hy−y2(2h−2y)=0\Rightarrow \dfrac{2}{{\sqrt {2hy - {y^2}} }}\left( {2h - 2y} \right) = 0
⇒2h−2y=0\Rightarrow 2h - 2y = 0
By rearranging, we get
y=hy = h
Therefore, the range of emerging stream will be maximum if y=h.y = h.
Therefore, from the above explanation correct option is (A) h.h.

Note: For maximum we need to have dRdy=0\dfrac{{dR}}{{dy}} = 0 and d2Rdy2<0\dfrac{{{d^2}R}}{{d{y^2}}} < 0 is important.
But calculating d2ydy2<0\dfrac{{{d^2}y}}{{d{y^2}}} < 0 is important.
When we get more than one values of y.y.
But there in this equation we got only one value of y,y, we can assume that it will be maximum at this point. Otherwise the question will not make any sense.