Question

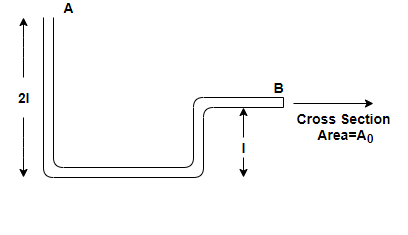
A tube in a vertical plane is shown in the figure. It is filled with a Liquid of density $\rho$and its end B is closed: Then the force exerted by the fluid on the tube at end B will be.: (Neglect atmospheric pressure and assume the radius of the tube to be negligible in comparison to l)

(A) $0$
(B) $\rho gl\mathop A\nolimits_0$
(C) $2\rho gl\mathop A\nolimits_0$
(D) cannot be determined

Answer 1

Hint:- The given problem can be solved by taking the consideration of variation of pressure for accelerated fluids. And force can be calculated by the knowledge of pressure at the given point and the cross section area of that point.

Complete step-by-step solution :
Step 1: As we know that pressure of liquid can be defined by the normal force (or thrust) exerted by the liquid at rest per unit area of the surface in contact with it, is called pressure of liquid or hydrostatic pressure.
So, as per above definition - $P = \dfrac{F}{A}$ and $F = PA$ where $P =$pressure, $F =$normal force exerted on object by liquid at surface in contact, and $A =$ area of object that is in contact of angle
As per given in the question the density of liquid filled in the tube is $\rho$ and the cross sectional area of tube at end B is $\mathop A\nolimits_0$.
So, force at the end B will be given by –
$\mathop F\nolimits_B = P \times A$ (1)
And according to Archimedes’ principle, pressure at point B will be given by –
$\Rightarrow \mathop P\nolimits_B = \rho \times g \times l$ (2)
Where $\rho =$ Density of the liquid which is filled in the tube
$g =$Gravity of earth
$l =$Height at which the point exists at which pressure/force to be calculated
Step 2: So from equation (1) and (2), force can be calculated at point B and that is given by –
$\Rightarrow \mathop F\nolimits_B = \rho gl \times \mathop A\nolimits_0 = \rho gl\mathop A\nolimits_0$
So, the force exerted by the fluid on the tube at end B will be $\mathop F\nolimits_B = \rho gl\mathop A\nolimits_0$.

So, the correct option is (B).

Note:-
Archimedes’ principle states that when a body is immersed completely or partly in a liquid at rest, it loses some of its weight. The loss in weight of the body in the liquid is equal to the weight of the liquid displaced by the immersed part of the body.
The same way we can see that pressure due to column of liquid of height h is given by $\mathop P\nolimits_B = \rho gl$.