Question
Question: A tube as shown below with constant cross-section throughout is filled with tube liquids for density...
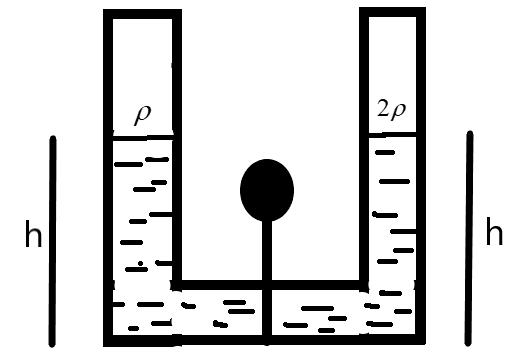
A tube as shown below with constant cross-section throughout is filled with tube liquids for density ρ and 2ρ separated by a line-plug. What happens to the height in each of the columns when this plug is removed?
Solution
We should understand the pressure difference due to the density difference in the two media separated by the plug. The density difference will change the height of the liquid column on the two sides of the tube which can be found from this information.
Complete answer:
We are given a U-shaped tube as shown in the figure.
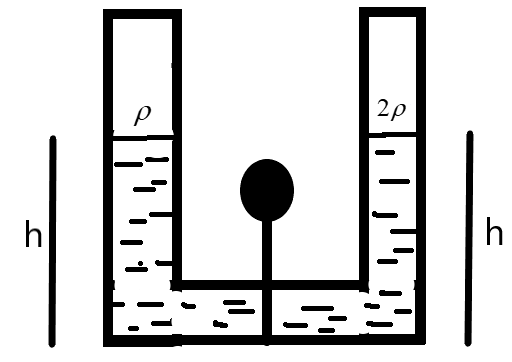
The two liquids of densities ρ and 2ρ are at an equal height ‘h’ divided by the plug as shown. Let ρ0 be the atmospheric pressure acting as the tube is kept open. The pressure on the left-side can be defined as –
P1=ρ0−ρgh
The right-side can be defined as –
P2=ρ0−2ρgh
The pressures at the same height are equal. This gives –
P1=P2
This is the situation when the height is the same.
Now, let us consider the condition when the plug is removed. In this case, there will be a pressure difference as the height attained will vary, such that –
