Question

A tube $1c{{m}^{2}}$in cross-section is attached to the top of a vessel 1cm high and area of cross-section $100c{{m}^{2}}$ . Water is poured into the system filling it to a depth of 100cm above the bottom of the vessel as shown in figure. Take, $g=10m{{s}^{-2}}$, then:

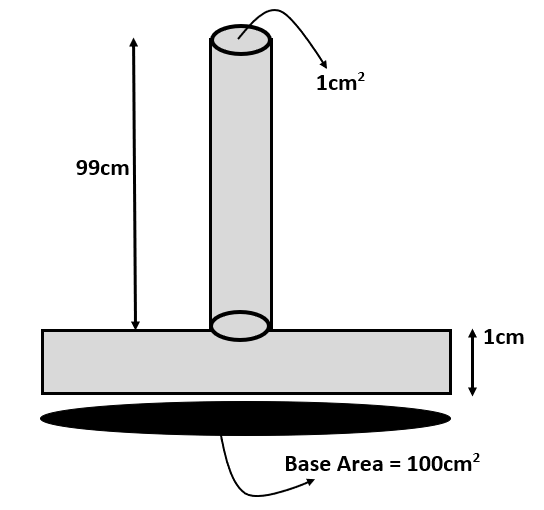
(A) force exerted by the water on the bottom of the vessel is 100N
(B) weight of water in the system is 1.99N
(C) both (A) and (B) are correct
(D) neither (A) nor (B) is correct

Answer 1

The force at the bottom of the vessel will be calculated by first calculating the pressure at that point and then by multiplying it with the base area of the vessel. Also, in the second case, the weight of water can be simply calculated by calculating the total mass of water and then multiplying it with gravitational acceleration.

Complete step-by-step answer:
Let us first assign some useful terms that we are going to use in our problem.
Let the pressure at the bottom of the vessel be given by ‘P’, then this pressure can be calculated as follows:
$\Rightarrow P=\rho \times g\times l$
Where,
$\rho$ is the density of water which is equal to $100gc{{m}^{-3}}$.
And, ‘l’ is the total length of water from the base that is equal to:
$\begin{aligned} & \Rightarrow l=100cm \\\ & \therefore l=1m \\\ \end{aligned}$
Thus, the pressure on the base of the vessel is:
$\begin{aligned} & \Rightarrow P=1000\times 10\times 1Pa \\\ & \therefore P={{10}^{4}}Pa \\\ \end{aligned}$
Thus, the force exerted by the water on the bottom of the vessel is equal to:
$\begin{aligned} & \Rightarrow F={{10}^{4}}\times (100\times {{10}^{-4}})N \\\ & \therefore F=100N \\\ \end{aligned}$ [First converting base into standard unit]
Hence, the force exerted by the water on the bottom of the vessel comes out to be 100N.
Now, for the weight of water, it can be calculated as follows:
$\Rightarrow W=\rho \times V\times g$
Where, ‘V’ is the total volume which is equal to:
$\begin{aligned} & \Rightarrow V=(100\times 1+99\times 1)c{{m}^{3}} \\\ & \Rightarrow V=199c{{m}^{3}} \\\ & \Rightarrow V=199\times {{10}^{-6}}{{m}^{3}} \\\ \end{aligned}$
Thus, the weight of water is:
$\begin{aligned} & \Rightarrow W=1000\times (199\times {{10}^{-6}})\times 10N \\\ & \therefore W=1.99N \\\ \end{aligned}$
Hence, the weight of water in the system is equal to 1.99N .
Hence, from our above calculation both the statements in option (A) and (B) are correct.

So, the correct answer is “Option C”.

Note: In this problem, while calculating the force due to water on the base, we used the base area of entire vessel and not the tube because the pressure is distributed over the entire area, that is, at the same height in a static fluid, the pressure is same at all the points.