Question

A truck travelling due north at $20m/s$ turns west and travels at the same speed. Then the change in velocity is
(A) $20\sqrt 2 m{s^{ - 1}}$ southwest
(B) $40m{s^{ - 1}}$southwest
(C) $20\sqrt 2 m{s^{ - 1}}$ northwest
(D) $40m{s^{ - 1}}$ northwest

Answer 1

Hint
Velocity is a vector quantity. So, with the change in direction, velocity is also changed even if the magnitude remains the same. We solve this question by representing the velocities given in the question as sides of a right-angle triangle and find the change in velocity using Pythagoras theorem.
Formula used: Pythagoras theorem ${H^2} = {A^2} + {B^2}$
Sides of a triangle are represented by $A,B$
The hypotenuse is represented by $H$

Complete step by step answer
Let the initial and final velocity be ${v_i}$ and ${v_f}$ respectively.
Change in velocity is the difference of initial velocity from final velocity, ${v_f} - {v_i} = {v_f} + ( - {v_i})$
The truck is first traveling from south to north and then takes a turn towards the west. The vectors for this are represented as

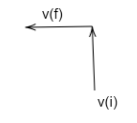
Since the change in velocity is final velocity minus the initial velocity, the position of vector changes,

The resultant of these two vectors is found by using Pythagoras theorem
$\Rightarrow \Delta {v^2} = {v_f}^2 + ( - v_i^2)$
The truck is traveling at $20m/s$
$\vartriangle v = \sqrt {{{20}^2} + {{20}^2}}$
$\Rightarrow \vartriangle v = 20\sqrt 2 m{s^{ - 1}}$
Since the truck starts from the south and goes towards the north and then turns west at the end, the direction is southwest.
Hence, option (A) $20\sqrt 2 m{s^{ - 1}}$ southwest is the correct answer.

Note
The method which is used in the question is also known as the triangle law of vector addition. This question can also be solved by writing the velocities in vector form and then using the formula for the resultant vector to find the change in velocity. Students might get confused while finding the direction of the change in velocity. The truck is moving from south to north and then turns towards the west. Hence the direction is taken as southwest.