Question

A truck traveling due to the north at 20m/s turns west and travels at the same speed. Find the change in velocity.

Answer 1

As we all know that velocity is a vector quantity and it is represented by vectors and hence to find the net result of two or more vectors, we generally add them by considering the fact that they are having directions also and then we put a negative or positive sign by considering the direction.

Complete Step-by-step Solution
In the northwest direction, velocity has a direction associated with it, if there is a change in speed it would be zero. But in the case when the truck turns in the west direction at the same speed as before its direction has changed from north to west.

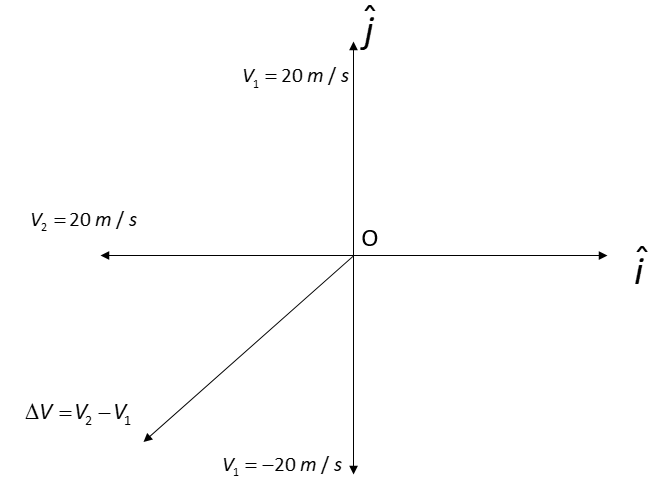
In the above diagram, the change is velocity must be ${V_2} - {V_1}$ which can clearly be represented by the above figure because as per the vector addition, the direction of ${V_1}$ has to be negative that is the velocity change could be written as,
$\Rightarrow \overrightarrow {\Delta V} = \overrightarrow {{V_2}} + \left( {\overrightarrow { - {V_1}} } \right)$
In the above figure, velocity has resolved into two components i.e. i and j along the x-axis and y-axis.
$\overrightarrow {{V_1}}$ is the initial velocity $= 20\hat j$
And $\overrightarrow {{V_2}}$ is the final velocity $= - 20\,\hat i$
So the change in velocity $\Delta \overrightarrow V {\rm{ }} = {\rm{ }}\overrightarrow {{V_2}} - \overrightarrow {{V_1}} = - 20(\hat i + \hat j)$
Now the magnitude of $\left| {\Delta V} \right| = \sqrt {{{\left( {20} \right)}^2} + {{\left( {20} \right)}^2}}$
$\Rightarrow \left| {\Delta V} \right| = 20\sqrt 2 m{s^{ - 1}}$
Here$\Delta {\rm{V}}$ is the change in velocity.

$\therefore$ The change in velocity is $20\sqrt 2 m{s^{ - 1}}$.

Note:
Velocity is defined as the rate of change of displacement with respect to time. It is a vector quantity. Vector quantities are those which show the magnitude and as well as direction. Also, the change in velocity can be determined by relative velocity and the Pythagoras theorem. Velocity always is negative, positive, and zero because zero velocity means no movement. It means when a body changes position the time is zero. It can happen when an object is thrown from the sky and no force is there to move upward, it seems to be motionless and velocity at that time is zero. Also, negative velocity shows here that the object is moving in the opposite direction.