Question
Question: A truck starts from resting at the top of a slope which is \[1m\] high and \[49m\] long. What is the...
A truck starts from resting at the top of a slope which is 1m high and 49m long. What is the acceleration and its speed at the bottom of the slope assuming friction is negligible?
Solution
We are asked to find the acceleration and speed at the bottom of a slope given that it is frictionless. We are only given the height and length of the slope. We start by finding the weight of the truck. Once we have found the weight of the truck, we can find the acceleration using Newton's second law of motion and from this, we can find the velocity as well.
Formula used: The formula to find the weight is given by W=Fsinθ
Newton's second law of motion states that a=mW
Newton's third equation gives the formula for speed as v=u2+2aS
Where m is the mass of the truck
θ is the angle between the ground and the slope
S is the displacement
u is the initial velocity
F is the force
Complete step by step answer:
We can find the value of work done by the truck to move down the slope using the formula,
W=Fsinθ
Substituting, W=Fsinθ=m×g×sinθ
But we know that the value of sine is given by dividing the length of opposite by the length of the hypotenuse.
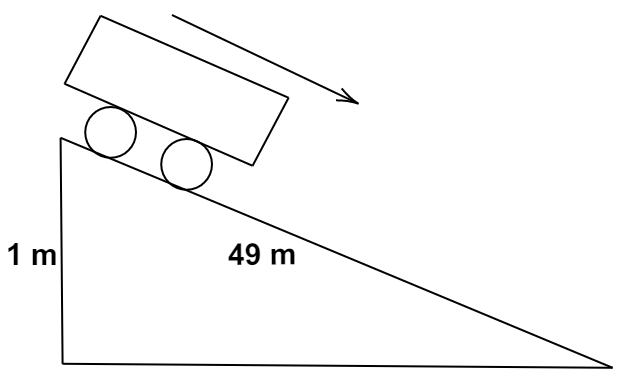
W=m×g×sinθ=491mg
We can now use this to find the value of acceleration using the formula a=mW
Substituting the values, we get a=mW=m491mg=491×9.8=0.2m/s2
Now we can move onto finding the value of velocity of the motion using the formula, v=u2+2aS
Substituting we get,
v=02+2(0.2)(49)=19.6
v=4.42 metres per second.
In conclusion the velocity of the motion is 4.42m/s and the acceleration is 0.2m/s2.
Note: Weight of a substance is the product of its mass and the acceleration due to gravity. Here we take the sine component or the sine value into the product as well because, the body is coming down the slope and the value of weight is not just normal to the surface, but the one that points down the slope.
