Question

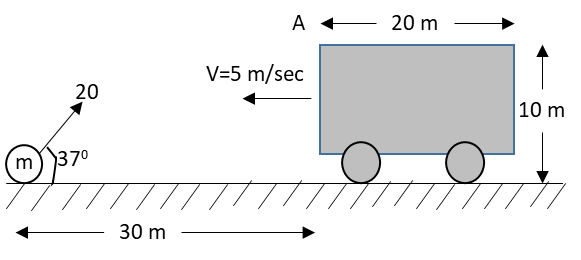
A truck of height $10m$ and length $20m$ is moving with a constant velocity of $v = 5m/\sec$ . A ball, $30m$ away from the truck, is projected with a velocity of $20m/\sec$ at an angle $37^\circ$ with horizontal. At how much distance from point A (top corner of the truck), will the ball strike the truck?

A. $2.86m$
B. $7.14m$
C. $3.86m$
D. None of these

Answer 1

Use the kinematic equation relating the displacement, initial velocity, acceleration and time of the object. First determine the horizontal displacements of the truck and the ball before the ball strikes the truck. From these displacements, determine the time at which this collision occurs. Then determine the vertical displacement of the ball and hence the distance from point A.

Formula used:
The kinematic equation for the displacement of an object is
$S = ut + \dfrac{1}{2}a{t^2}$ …… (1)
Here, S is displacement, u is initial velocity, a is acceleration and t is time.

Complete step by step answer:
We have given that the distance between the truck and the ball is $30m.$
We can assume the truck and the ball covers the distances ${S_1}$ and ${S_2}$ before colliding with each other respectively. So, the sum of the distances ${S_1}$ and ${S_2}$is $30m.$.
${S_1} + {S_2} = 30m$ …… (2)
If ${u_1}$ is the initial velocity of the truck then the distance covered in time $t$ is given by
${S_1} = {u_1}t$
The initial velocity of the truck is $5\,m/\sec$.
${u_1} = 5\,m/\operatorname{s}$
Substitute for ${u_1}$ in the above equation.
${S_1} = 5t$
The angle of projection of the ball is $37^\circ$ and velocity of projection of the ball is $20m/\sec$.
$\theta = 37^\circ$
${u_2} = 20m/\sec$
The displacement of the ball in time $t$ can be determined by using equation (1)
Rewrite equation (1) for the horizontal displacement of the ball.
${S_2} = {u_{2x}}t + \dfrac{1}{2}{a_{2x}}{t^2}$
During the horizontal motion of the ball, the horizontal component of velocity ${u_{2x}}$ remains the same all the time. Hence, the horizontal acceleration ${a_2}$ of the ball is zero.
${a_{2x}} = 0\,{\text{m/}}{{\text{s}}^2}$
Also,
${u_{2x}} = {u_2}\cos \theta$
$\Rightarrow {u_{2x}} = 20\cos 37^\circ$
Substitute $20\cos 37^\circ$ for ${u_{2x}}$ and $0\,{\text{m/}}{{\text{s}}^2}$ for ${a_{2x}}$ in the above equation.
${S_2} = \left( {20\cos 37^\circ } \right)t + \dfrac{1}{2}\left( {0\,{\text{m/}}{{\text{s}}^2}} \right){t^2}$
$\Rightarrow {S_2} = 20\cos 37^\circ t$
Substitute $20\cos 37^\circ t$ for ${S_1}$ and $20\cos 37^\circ t$ for ${S_2}$ in equation (2).
$\left( {5t} \right) + \left( {20\cos 37^\circ t} \right) = 30m$
$\Rightarrow \left( {5 + 20\cos 37^\circ } \right)t = 30m$
$\Rightarrow t = \dfrac{{30}}{{5 + 20\cos 37^\circ }}$
$\Rightarrow t = 1.43\,{\text{s}}$
Hence, the time in which the truck and the ball covers the horizontal distance required for their collision is $1.43\,{\text{s}}$.
Determine the vertical displacement of the ball in time $t$.
The vertical component of velocity of the ball is
${u_{2y}} = {u_2}\sin \theta$
$\Rightarrow {u_{2y}} = 20\sin 37^\circ$
The vertical acceleration of the ball is equal to the acceleration due to gravity in the downward direction. Hence, has the value $- g$.
${a_{2y}} = - g$
Rewrite equation (1) for the vertical displacement of the ball.
${S_{2y}} = {u_{2y}}t + \dfrac{1}{2}{a_2}{t^2}$
Substitute $20\sin 37$ for ${u_{2y}}$, $- g$ for ${a_{2y}}$ and $1.43\,{\text{s}}$ for $t$ in the above equation.
${S_{2y}} = \left( {20\sin 37} \right)\left( {1.43\,{\text{s}}} \right) + \dfrac{1}{2}\left( { - g} \right){\left( {1.43\,{\text{s}}} \right)^2}$
$\Rightarrow {S_{2y}} = \left( {20\sin 37^\circ } \right)\left( {1.43\,{\text{s}}} \right)\dfrac{1}{2}\left( {9.8\,{\text{m/}}{{\text{s}}^2}} \right){\left( {1.43\,{\text{s}}} \right)^2}$
$\Rightarrow {S_{2y}} = 7.14\,{\text{m}}$
Hence, the vertical displacement of the ball when it hits the truck is $7.14\,{\text{m}}$.
The distance of the ball from point A is $10\,{\text{m}} - 7.14\,{\text{m}} = 2.86\,m$.
Therefore, the ball will strike the truck at a distance $2.86\,m$ from point A.

Hence, the correct option is A.

Note:
The students should keep in mind that the horizontal component of velocity of the ball in projectile motion remains always uniform and constant. Hence, the horizontal component of acceleration of the ball is zero. Also, the students should use the vertical component of acceleration which is equal to acceleration due to gravity with a negative sign. If the values of acceleration are not used properly, then the final answers will not be correct.