Question

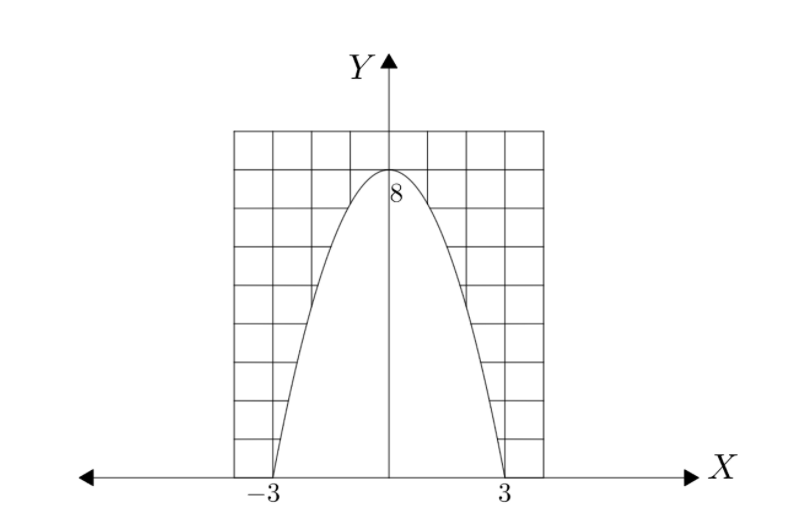
A truck carrying a wide load needs to pass through the parabolic tunnel shown. The units are metres.
The truck is $5{\text{ }}m$ high and $4{\text{ }}m$ wide.
I.Find the quadratic function which describes the shape of the tunnel.
II.Determine whether the truck will fit.

Answer 1

Hint : For the equation of the tunnel, firstly we will consider a generalized equation of the shape of the tunnel. Then according to the given curve, we will improvise the generalized equation. Finally we will answer the first part of the question.
For the second part, we will compare the dimensions of the truck with the coordinates of the parabola passing through the coordinate axes. Then, we will finally answer the second part of the question.
Formula Used:
General Equation of a parabola:
$(y{\text{ }} - {\text{ }}h){\text{ }} = {\text{ }}4{\text{ }} \times {\text{ }}a{\text{ }} \times {\text{ }}{(x{\text{ }} - {\text{ }}k)^2}$
Length of the latus rectum:
$4{\text{ }} \times {\text{ }}a$

Complete step-by-step answer :
Now,
We can clearly see that the tunnel is in the form of a parabola;
Thus, the generalized formula of the tunnel is:
$(y{\text{ }} - {\text{ }}h){\text{ }} = {\text{ }}4{\text{ }} \times {\text{ }}a{\text{ }} \times {\text{ }}{(x{\text{ }} - {\text{ }}k)^2}$
Now,
Since the base passes through the points,
$(3,0)$ and $( - 3,0)$.
Thus,
The base length or the length of the latus rectum is
$(3{\text{ }} - {\text{ }}( - 3)){\text{ }} = {\text{ }}6{\text{ }}units$
Also,
The formula of latus rectum is:
$4{\text{ }} \times {\text{ }}a$
Hence,
The value of $a$ can be evaluated as,
$4{\text{ }} \times {\text{ }}a{\text{ }} = {\text{ }}6$
After further evaluation, we get
$a{\text{ }} = {\text{ }}\dfrac{3}{2}$
Now,
The tunnel is in the form of an inverted parabola.
Thus,
The value of $a$ is negative.
Thus,
$a{\text{ }} = {\text{ }}\dfrac{{ - {\text{ }}3}}{2}$
Now,
The generalized formula of the parabola is:
$(y{\text{ }} - {\text{ }}h){\text{ }} = {\text{ }}4{\text{ }} \times {\text{ }}a{\text{ }} \times {\text{ }}{(x{\text{ }} - {\text{ }}k)^2}$
Putting in the value of $a$, we get
$(y{\text{ }} - {\text{ }}h){\text{ }} = {\text{ }}4{\text{ }} \times {\text{ }}\dfrac{{ - 3}}{2}{\text{ }} \times {\text{ }}{(x{\text{ }} - {\text{ }}k)^2}$
After further evaluation, we get
$(y{\text{ }} - {\text{ }}h){\text{ }} = {\text{ }} - {\text{ }}6{\text{ }} \times {\text{ }}{(x{\text{ }} - {\text{ }}k)^2}{\text{ }} - - - - - - - - - - - {\text{ }}(i)$
Now,
As the parabola is moved $8{\text{ }}units$ in the $y - {\text{ }}axis$.
Thus,
The value of $h{\text{ }} = {\text{ }}8$
Then,
The equation $(i)$ transforms to
$(y{\text{ }} - {\text{ }}8){\text{ }} = {\text{ }} - 6{\text{ }} \times {\text{ }}{(x{\text{ }} - {\text{ }}k)^2}{\text{ }} - - - - - - - - - - - {\text{ }}(ii)$
Again,
The parabola is lying on the $y - {\text{ }}axis$.
Thus,
The parabola is moved $0{\text{ }}units$ in the $x - {\text{ }}axis$.
Then,
The value of $k{\text{ }} = {\text{ }}0$
Thus,
The equation $(ii)$ transforms to
$(y{\text{ }} - {\text{ }}8){\text{ }} = {\text{ }} - 6{\text{ }} \times {\text{ }}{(x{\text{ }} - {\text{ 0}})^2}$
After further evaluation, we get
$(y{\text{ }} - {\text{ }}8){\text{ }} = {\text{ }} - 6{\text{ }} \times {\text{ }}{x^2}{\text{ }} - - - - - - - - {\text{ }}(iii)$
After further evaluation, we get
$6{x^2}{\text{ }} + {\text{ }}y{\text{ }} - {\text{ }}8$
Thus,
The equation of the tunnel is
$6{x^2}{\text{ }} + {\text{ }}y{\text{ }} - {\text{ }}8$
Now,
For the second part, we will compare the dimensions of the tunnel with the dimensions of the truck.
Clearly,
The tunnel is
$(3{\text{ }} - {\text{ }}( - 3)){\text{ }} = {\text{ }}6{\text{ }}m$
Also,
The tunnel is
$(8{\text{ }} - {\text{ }}0){\text{ }} = {\text{ }}8{\text{ }}m$
Also,
Given that
The truck is $5{\text{ }}m$ high and $4{\text{ }}m$ wide.
Now,
Clearly the tunnel is wider as well as higher than the truck.
Thus,
The truck will easily pass through the tunnel.
Hence,
The answers are
The quadratic function which describes the shape of the tunnel is $6{x^2}{\text{ }} + {\text{ }}y{\text{ }} - {\text{ }}8$
The truck will easily pass through the tunnel.

Note : Students often mistake that the transformed equation of the parabola will be that the coordinate of the intersection will directly lie with the coordinate variable but they should remember that the opposite sign would lie. For example, if the curve cuts the $y - {\text{ }}axis$ at $+ {\text{ }}7$, then the equation will transform to $(y{\text{ }} - {\text{ }}7)$ rather than $(y{\text{ }} + {\text{ }}7)$.
Students should be cautious of the above mentioned point with all the variables involved.