Question

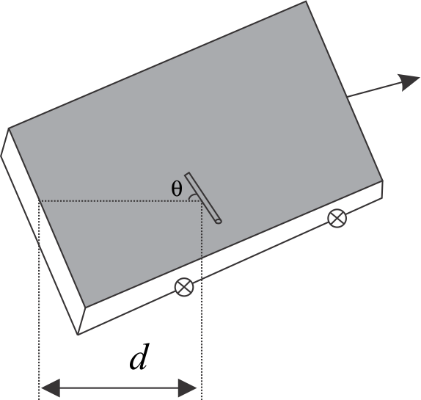
A trolley is at rest initially with solid cylinder placed on its bed such that cylinder axis makes an angle $\theta$ with the direction of motion of trolley as shown in the figure starts to move forward with constant acceleration $a.$ It is given that the initial distance of mid – point of cylinder axis from rear edge of trolley bed is $d$, find the distance $s$ which the trolley goes before the cylinder rolls off the edge of its horizontal bed. Also find the frictional force which acts on the cylinder. Neglect the slipping and assume dimensions of the cylinder to be very small as compared to other dimensions.

Answer 1

First, calculate horizontal forces then, take a moment about the cylinder axis then, find the expression for $r\alpha$ using expressions of horizontal forces.
Now, use the second equation of motion -
Then, calculate $t$ by putting the values in their respective places.
Find the total frictional force acting on the cylinder.

Complete step by step solution:

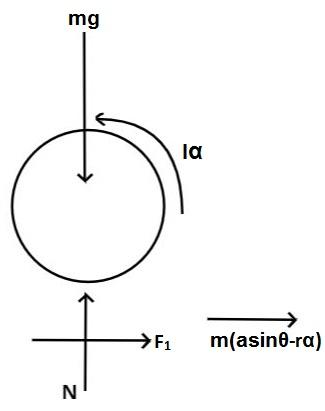
Therefore, net acceleration of the cylinder axis is $a\sin \theta - r\alpha$ normal to the axis.
Consider free diagram of the cylinder as shown in the figure –
${F_2} = m\alpha \sin \theta$
In the figure, forces act normal to the cylinder axis so, ${F_2}$ is not shown in the free body diagram.
Now, for horizontal forces –
${F_1} = m\left( {a\sin \theta - r\alpha } \right) \cdots (1)$
Now, taking moment about cylinder axis –
${F_1}r = I\alpha$
We know that –
$I = \dfrac{{m{r^2}}}{2}$
Putting the value of $I$ in the moment about cylinder axis –
$\Rightarrow {F_1} = \dfrac{1}{2}mr\alpha \cdots (2)$
From equation $(1)$ and equation $(2)$, we get –
$\Rightarrow r\alpha = \dfrac{2}{3}a\sin \theta \cdots (3)$
The cylinder will roll off the edge of the trolley bed when its centre of mass reaches the edge. Since, the cylinder axis is inclined at an angle $\theta$ with direction of motion of trolley, therefore, its centre of mass follows a straight - line path relative to the trolley bed, and that straight - line is normal to cylinder axis. Hence, displacement of centre of mass of the cylinder, relative to trolley is equal to $d cosec \theta$.
Because the trolley is initially at rest –
$\therefore u = 0$
Now, acceleration $= r\alpha = \dfrac{2}{3}a\sin \theta$
Distance, $s = d cosec \theta$
Using, $s = ut + \dfrac{1}{2}a{t^2},t = \sqrt {\dfrac{{3d}}{{a{{\sin }^2}\theta }}}$
Now considering motion of trolley during this interval of time, $u = 0$ and acceleration $= a$
Using the value of $t$ in the formula of $s$, we get –
$\Rightarrow s = \dfrac{3}{2}d\cos e{c^2}\theta$
We know that,
$\Rightarrow {F_1} = \dfrac{1}{2}mr\alpha$
From equation $(3)$, we get –
$\Rightarrow {F_1} = \dfrac{1}{3}ma\sin \theta$
Now, the total frictional force acting on the cylinder is –
$F = \sqrt {F_1^2 + F_2^2} \\\ \Rightarrow F = \dfrac{1}{3}ma\sqrt {{{\sin }^2}\theta + 9{{\cos }^2}\theta } \\\$
Hence, this is the required expression of frictional force.

Note: Due to angular acceleration cylinder axis has acceleration relative trolley bed, which will be equal to $r\alpha$ normal to cylinder axis. But component of accelerations of trolley normal to cylinder axis is $\sin \theta$so, the net acceleration of cylinder axis is .$a\sin \theta - r\alpha$.