Question
Question: A triangular plate of uniform thickness and density is made to rotate about an axis perpendicular to...
A triangular plate of uniform thickness and density is made to rotate about an axis perpendicular to the paper and (a) passing through A, (b) passing through B, by the application of some force F at C (midpoint of AB) as shown in fig. in which case is angular acceleration more
(A) in case (a)
(B) in case (b)
(C) both (a) and (b)
(D) none of these
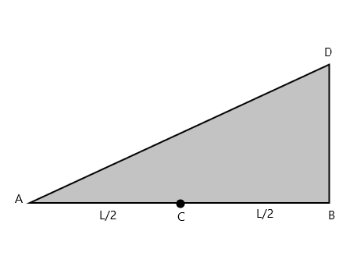
Solution
Since, the force is constant, the torque in the case of a) and b) are the same. The moment of inertia is lowest for the axis about B.
Formula used: In this solution we will be using the following formulae; T=Iω where T is the torque acting on a body, I is the moment of inertia of the body, and ω is the angular acceleration of the body
Complete step by step answer:
We are given a triangular plate which has a uniform density
To solve the above, we have that at point C (case c), the torque acting on the body is half as much as the torque acting in case a) and b).
To tell which is the one with the higher angular acceleration, we recall the formula
T=Iω where T is the torque acting on a body, I is the moment of inertia of the body, and ω is the angular acceleration of the body. Hence, we have that
ω=IT
This signifies that for a higher angular acceleration, the torque has to be high and at the same time the moment of inertia has to be low.
Now, it is already established that the torque about C is the lowest.
For the moment of inertia, the lowest is about point B. Hence, point C cannot have the highest angular acceleration.
Now, since a and b have the same torque but with case b) having the lowest inertial, we conclude that case b) has the highest angular acceleration.
Note:
For clarity, we say the moment of inertia is lowest in case b because the moment of inertia is the amount of mass being moved about an axis. About point B, the majority of the body (hence mass) of the triangle is moving through a short distance as compared to moment about point A.
