Question

A triangular loop of side $l$ carries a current i. It is placed in a magnetic field B such that the plane of the loop is in direction of B. The torque on the loop is:
A) $iBl$
B) ${i^2}Bl$
C) $\dfrac{{\sqrt 3 }}{4}Bi{l^2}$
D) $infinity$

Answer 1

The current carrying conductor experiences a force when it is placed in an external magnetic field. If equal force is applied on the ends of a current carrying conductor separated by a distance, there is rotation caused in the current carrying conductor due to a quantity called torque.

Complete step by step solution:
When a current carrying conductor is placed in an external magnetic field, a force is applied on the conductor equal to,
$F = BIL\sin \theta$
where,
B = magnetic field
I = current in the conductor
L = length of the conductor
$\theta$ = relative angle between the direction of magnetic field and the current carrying conductor.
If we consider a loop carrying conductor, this equal force acting on the loop about its centroid, causes a rotational effect on the loop, which is measured by the quantity called torque.
Torque is the product of magnitude of force and the distance of separation between the points where force is applied.
If we consider a loop of area A with current flowing I and placed in a magnetic field B, the torque acting on the loop is given by the formula –
$\tau = IAB$
where I = current, A = area of loop, B = magnetic field.
Consider a triangle loop of length $l$ carrying current $i$ with the direction of magnetic field B as follows:

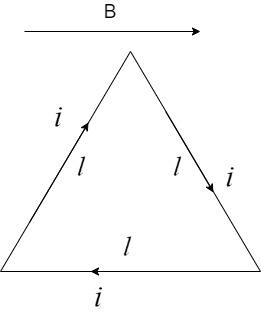
The area of the triangle is given by the formula –
$\Rightarrow A = \dfrac{{\sqrt 3 }}{4}{l^2}$
The torque acting on the loop is given by –
$\Rightarrow \tau = iAB$
Substituting the value of area A in the above expression , we have –
$\Rightarrow \tau = \dfrac{{\sqrt 3 }}{4}iB{l^2}$

Hence, the correct option is Option C.

Note: In this problem, the triangular loop has only one turn. The torque on the loop is directly proportional to the number of turns in the loop. Hence, torque acting on a loop with N number of turns is given by –
$\tau = NIAB$.