Question

A triangular glass prism with apex angle $\phi = {60.0^0}$ has an index of refraction $n = 1.50$ what is the smallest angle of incidence ${\theta _1}$ for which a light ray can emerge from the other side?

Answer 1

In order to solve this question, we will use the Snell’s law of refraction which is stated as “the ratio of $\sin$ of angle of incidence to $\sin$ of angle of refraction is a constant called refractive index of a material”$\mu = \dfrac{{\sin {\theta _1}}}{{\sin {\theta _2}}}$.

Complete step by step answer:
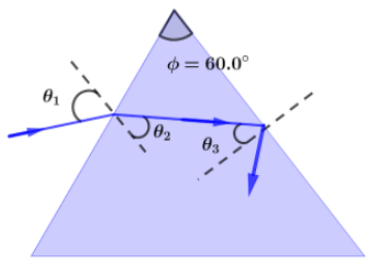
Let us first trace the reflected ray inside the glass prism and mark different angles between normal and reflected, refracted rays in the diagram. Let refracted ray makes an angle of ${\theta _2}$ with the normal and Reflected ray inside the glass prism makes an angle of ${\theta _3}$ with the normal. And given that,
$\mu = 1.50 \\\ \Rightarrow \phi = {60^0}$
Now from Snell’s law, applying for refraction in first interface of glass prism
$\mu = \dfrac{{\sin {\theta _1}}}{{\sin {\theta _2}}}$
$\dfrac{{\sin {\theta _1}}}{{\sin {\theta _2}}} = 1.5 \to (i)$

Now, the angle of incidence at the second interface is ${\theta _3}$ which must be lesser than the critical angle of the glass prism in order to emerge from the other side. So, ${\theta _3} < {\theta _c}$. Now, we know critical angle of any material is related with its refractive index as
${\theta _c} = {\sin ^{ - 1}}(\dfrac{1}{\mu })$
Using $n = 1.50$ $n$ also represents refractive index,
${\theta _c} = {\sin ^{ - 1}}(\dfrac{1}{{1.5}}) \\\ \Rightarrow {\theta _c} = {41.8^0}$
$\Rightarrow {\theta _3} < {41.8^0}$

Now, as from the diagram we can see that ${\theta _2},{\theta _3}$ are related as,
$({90^ \circ } - {\theta _2}) + ({90^ \circ } - {\theta _3}) + {60^ \circ } = {180^0} \\\ \Rightarrow {\theta _2} = {60^0} - {\theta _3} \to (ii) \\\$
Now, to avoid total internal reflection at second interface of glass prism,
${\theta _3} < {41.8^0} \\\ \Rightarrow {\theta _2} > 60 - 41.8 \\\ \Rightarrow {\theta _2} > {18.2^0}$
Now just putting above value in equation $\dfrac{{\sin {\theta _1}}}{{\sin {\theta _2}}} = 1.5$
We get,
$\sin {\theta _1} > 1.5 \times \sin {18.2^0} \\\ \therefore {\theta _1} > {27.9^0} \\\$
Hence, the smallest angle is ${\theta _1} > {27.9^0}$ to which light will emerge from the prism at the other side.

Note: We should know that Total internal reflection is the phenomenon in which a light ray gets completely reflected within the medium, and there is particular angle below which Total internal reflection doesn’t takes place called critical angle which is related with index of refraction of that material as $n = \dfrac{1}{{\sin {\theta _c}}}$.