Solveeit Logo
Login

Question

Question: A triangular block of mass M with angles \(30^\circ \), \(60^\circ \) and \(90^\circ \)rests with it...

A triangular block of mass M with angles 30∘30^\circ , 60∘60^\circ and 90∘90^\circ rests with its 30∘−90∘30^\circ - 90^\circ side on a horizontal table. A cubical block of mass m rests on the60∘−30∘60^\circ - 30^\circ side. The acceleration, which M must have relative to the table, to keep m stationary relative to the triangular block, (assuming frictionless contact) is.

  1. g
  2. g2\dfrac{g}{{\sqrt 2 }}
  3. g3\dfrac{g}{{\sqrt 3 }}
  4. g5\dfrac{g}{{\sqrt 5 }}
Explanation

Solution

This is a very similar question of a block mass “m” on a hill, the only difference is that the hill is moving, here instead of a hill a triangular block of mass “M” is given. Draw a free body diagram in which all the vertical and horizontal forces are mentioned and divide the vertical net force by the horizontal net force.

Complete step by step solution:


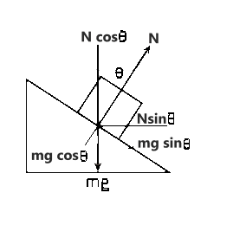
The net force in the vertical direction will be zero because there is no acceleration.
∑Fy=0\sum {{F_y}} = 0 ;
Ncos⁡θ=mgN\cos \theta = mg;
Now, in the horizontal direction the surface is frictionless so:
mgsin⁡θ=0mg\sin \theta = 0 ;

Therefore, the force is acting on the forward side in the horizontal direction:
Nsin⁡θ=FxN\sin \theta = {F_x};
Now, according to Newton’s second law force equals mass times acceleration:
Nsin⁡θ=maN\sin \theta = ma;
Divide the vertical force Fy{F_y} by horizontal forceFx{F_x}:
Nsin⁡θNcos⁡θ=mamg\dfrac{{N\sin \theta }}{{N\cos \theta }} = \dfrac{{ma}}{{mg}};
⇒sin⁡θcos⁡θ=ag\Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{a}{g};
Write the above equation in terms of a:
⇒tan⁡θ=ag\Rightarrow \tan \theta = \dfrac{a}{g};
⇒a=gtan⁡θ\Rightarrow a = g\tan \theta;
Here, the cube is inclined at angle of 30∘30^\circ with the base of the triangle so:
⇒a=gtan⁡30\Rightarrow a = g\tan 30;
⇒a=g3\Rightarrow a = \dfrac{g}{{\sqrt 3 }};

Final Answer: Option “3” is correct. Therefore, the acceleration, which M must have relative to the table, to keep m stationary relative to the triangular block is g3\dfrac{g}{{\sqrt 3 }};

Note: Here, be careful while resolving the horizontal and vertical forces. In equating vertical forces, the normal resolved force “Ncos⁡θN\cos \theta ” is equal to mg and not equal to mgcos⁡θmg\cos \theta and similarly in equating the horizontal forces mgsin⁡θmg\sin \theta will be equal to the frictional force and since the frictional force is zero therefore mgsin⁡θmg\sin \theta will be zero. Equate the horizontal force Fx{F_x} with the normal resolved horizontal force Nsin⁡θN\sin \theta .