Question

A triangle has vertices $\left( {6,3} \right)$, $\left( {5,8} \right)$ and $\left( {3,2} \right)$. What is the area of a triangle's circumscribed circle?

Answer 1

A circle circumscribing a triangle is a circle that passes through the vertices of a triangle. We know, the equation of a circle is given by ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$, where $\left( {h,k} \right)$ is the centre of a circle where $h$ is the $x$ coordinate of the centre of circle and $k$ is the $y$ coordinate of the centre of circle. $r$ is the radius of the circle. Now, to solve this question, we will substitute the given points in the equation of the circle as they lie on the circle and then solve these equations to find the value of $r,g$ and $h$. After finding the value of $r$ i.e. the radius of the circle, we will find the area of the circle using the formula: Area of the circle $= \pi {r^2}$, where $r$ is the radius of the circle.

Complete step by step answer:
We are given three vertices of a triangle and we need to find the area of the circle circumscribing this triangle. Let us first draw the figure for the given question.

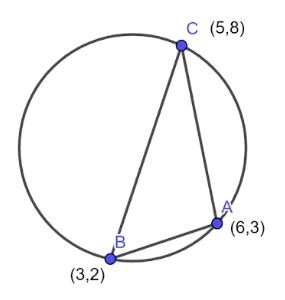
Here we see that the vertices of the triangle lie on the circle and so they will satisfy the equation of the circle. The given points are $\left( {6,3} \right)$, $\left( {5,8} \right)$ and $\left( {3,2} \right)$.

We know, the equation of a circle is given by
${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$
where $h$ is the $x$ coordinate of the centre of circle and $k$ is the $y$ coordinate of the centre of the circle and $r$ is the radius of the circle.
Now, substituting the given points in the equation one by one.
First, substituting $\left( {6,3} \right)$ in ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$, we get
$\Rightarrow {\left( {6 - h} \right)^2} + {\left( {3 - k} \right)^2} = {r^2}$
Now, using the identity ${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$, we get
$\Rightarrow \left( {{{\left( 6 \right)}^2} + {{\left( h \right)}^2} - 2 \times 6 \times h} \right) + \left( {{{\left( 3 \right)}^2} + {{\left( k \right)}^2} - 2 \times 3 \times k} \right) = {r^2}$
Now, solving the brackets, we get
$\Rightarrow \left( {36 + {h^2} - 12h} \right) + \left( {9 + {k^2} - 6k} \right) = {r^2}$
Opening the brackets, we get
$\Rightarrow 36 + {h^2} - 12h + 9 + {k^2} - 6k = {r^2}$

Adding the constant terms, we get
$\Rightarrow {h^2} - 12h + {k^2} - 6k + 45 = {r^2} - - - - - - (1)$
Now, substituting $\left( {5,8} \right)$ in ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$, we get
$\Rightarrow {\left( {5 - h} \right)^2} + {\left( {8 - k} \right)^2} = {r^2}$
Again, using the identity ${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$, we get
$\Rightarrow \left( {{{\left( 5 \right)}^2} + {{\left( h \right)}^2} - 2 \times 5 \times h} \right) + \left( {{{\left( 8 \right)}^2} + {{\left( k \right)}^2} - 2 \times 8 \times k} \right) = {r^2}$
Solving the brackets now,
$\Rightarrow \left( {25 + {h^2} - 10h} \right) + \left( {64 + {k^2} - 16k} \right) = {r^2}$
Now, opening the brackets, we get
$\Rightarrow 25 + {h^2} - 10h + 64 + {k^2} - 16k = {r^2}$

Now, adding the constant terms together,
$\Rightarrow {h^2} - 10h + {k^2} - 16k + 89 = {r^2} - - - - - - (2)$
Now, substituting $\left( {3,2} \right)$ in ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$, we get
$\Rightarrow {\left( {3 - h} \right)^2} + {\left( {2 - k} \right)^2} = {r^2}$
Using the identity ${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$, we get
$\Rightarrow \left( {{{\left( 3 \right)}^2} + {{\left( h \right)}^2} - 2 \times 3 \times h} \right) + \left( {{{\left( 2 \right)}^2} + {{\left( k \right)}^2} - 2 \times 2 \times k} \right) = {r^2}$
Now, solving the brackets, we get
$\Rightarrow \left( {9 + {h^2} - 6h} \right) + \left( {4 + {k^2} - 4k} \right) = {r^2}$
Opening the brackets, we get
$\Rightarrow 9 + {h^2} - 6h + 4 + {k^2} - 4k = {r^2}$

Now, adding the constant term together, we get
$\Rightarrow {h^2} - 6h + {k^2} - 4k + 13 = {r^2} - - - - - - (3)$
Now, subtracting (2) from (3), we have
$\Rightarrow \left( {{h^2} - 6h + {k^2} - 4k + 13} \right) - \left( {{h^2} - 10h + {k^2} - 16k + 89} \right) = {r^2} - {r^2}$
Opening brackets, we get
$\Rightarrow {h^2} - 6h + {k^2} - 4k + 13 - {h^2} + 10h - {k^2} + 16k - 89 = {r^2} - {r^2}$
Collecting the like terms together and cancelling out some terms, we get
$\Rightarrow \left( {10h - 6h} \right) + \left( {16k - 4k} \right) + \left( {13 - 89} \right) = 0$
Now, solving the brackets, we get
$\Rightarrow 4h + 12k + \left( { - 76} \right) = 0$
$\Rightarrow 4h + 12k - 76 = 0$

Dividing the whole equation by $4$, we get
$\Rightarrow h + 3k - 19 = 0 - - - - - - (4)$
Now, subtracting (1) form (2), we get
$\Rightarrow \left( {{h^2} - 10h + {k^2} - 16k + 89} \right) - \left( {{h^2} - 12h + {k^2} - 6k + 45} \right) = {r^2} - {r^2}$
Opening the brackets, we get
$\Rightarrow {h^2} - 10h + {k^2} - 16k + 89 - {h^2} + 12h - {k^2} + 6k - 45 = {r^2} - {r^2}$
Now, collecting the like terms together and cancelling out some terms, we get
$\Rightarrow \left( {12h - 10h} \right) + \left( {6k - 16k} \right) + \left( {89 - 45} \right) = 0$
Solving the brackets, we get
$\Rightarrow 2h + \left( { - 10k} \right) + 44 = 0$
$\Rightarrow 2h - 10k + 44 = 0$

Now, dividing the whole equation by $2$, we get
$\Rightarrow h - 5k + 22 = 0 - - - - - - - (5)$
Now, subtracting (4) from (5), we have
$\Rightarrow \left( {h - 5k + 22} \right) - \left( {h + 3k - 19} \right) = 0 - 0$
Opening the brackets, we have
$\Rightarrow h - 5k + 22 - h - 3k + 19 = 0 - 0$
Cancelling out some terms and collecting the like terms together, we have
$\Rightarrow \left( { - 5k - 3k} \right) + \left( {22 + 19} \right) = 0 - 0$
Solving the brackets, we get
$\Rightarrow - 8k + 41 = 0$
Rearranging the terms, we get
$\Rightarrow 8k = 41$
$\Rightarrow k = \dfrac{{41}}{8} - - - - - - (6)$

Substituting $k = \dfrac{{41}}{8}$ in (5), we get
$\Rightarrow h - 5\left( {\dfrac{{41}}{8}} \right) + 22 = 0$
$\Rightarrow h - \dfrac{{205}}{8} + 22 = 0$
Shifting the constant term to the right hand side, we get
$\Rightarrow h = \dfrac{{205}}{8} - 22$
Taking LCM on the right hand side, we get
$\Rightarrow h = \dfrac{{205 - 22\left( 8 \right)}}{8}$
$\Rightarrow h = \dfrac{{205 - 176}}{8}$
Now, solving the right hand side, we get
$\Rightarrow h = \dfrac{{29}}{8} - - - - - - (7)$
Substituting (6) and (7) in (2), we get
$\Rightarrow {\left( {\dfrac{{29}}{8}} \right)^2} - 10\left( {\dfrac{{29}}{8}} \right) + {\left( {\dfrac{{41}}{8}} \right)^2} - 16\left( {\dfrac{{41}}{8}} \right) + 89 = {r^2}$
Now, solving the brackets, we get
$\Rightarrow \dfrac{{841}}{{64}} - \dfrac{{290}}{8} + \dfrac{{1681}}{{64}} - \dfrac{{656}}{8} + 89 = {r^2}$

Taking LCM, we get
$\Rightarrow \dfrac{{841 - 290\left( 8 \right) + 1681 - 656\left( 8 \right) + 89\left( {64} \right)}}{{64}} = {r^2}$
$\Rightarrow \dfrac{{841 - 2320 + 1681 - 5248 + 5696}}{{64}} = {r^2}$
Solving the numerator, we get
$\Rightarrow \dfrac{{650}}{{64}} = {r^2}$
After simplifying, we get
$\Rightarrow \dfrac{{325}}{{32}} = {r^2} - - - - - - (8)$
Hence, we got the square of radius of the circle. i.e. ${r^2}$
Now, area of the circle is given by $\pi {r^2}$
Using (8), we get
Area of the circle $= \pi {r^2}$
$\Rightarrow$ Area of the circle $= \pi \dfrac{{325}}{{32}}$
$\therefore$ Area of the circle $= \dfrac{{325\pi }}{{32}}$

Hence, we got the area of the circle as $\dfrac{{325\pi }}{{32}}$.

Note: Alternatively, We could have used the formula ${r^2} = \dfrac{{{a^2}{b^2}{c^2}}}{{16{A^2}}}$, where $r$ is the radius of the circumcircle, $a,b,c$ are the lengths of the sides of the triangle circumscribed in the circle and $A$ is the area of the triangle. We can find the length of the side of the triangle when two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are given by using the formula $\sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}}$.