Question
Question: A triangle has given base and a given perimeter. Then the vertical angle is greatest when the triang...
A triangle has given base and a given perimeter. Then the vertical angle is greatest when the triangle.
A
Is equilateral
B
Is isosceles
C
Has different side
D
None of these
Answer
Is isosceles
Explanation
Solution
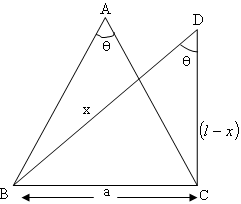
cosθ=2x(l−x)x2+(l−x)2−a2=T
T=2lx−2x2x2+l2+x2−2lx−a2
⇒ T=2lx−2x22x2−2lx+l2−a2 = −1+21(xl−x2l2−a2)
⇒ dxdt=−21(lx−x2)2(l−2x)(l2−a2)=0 ; x=2l
'θ' is maximum when x=2l triangle is an isosceles.
So 'b' is correct