Solveeit Logo
Login

Question

Question: A triangle ABC is placed so that the mid-points of the sides are on the x,y,z axes. Lengths of the i...

A triangle ABC is placed so that the mid-points of the sides are on the x,y,z axes. Lengths of the intercepts made by the plane containing the triangle on these axes are respectively α,β,γ\alpha ,\beta ,\gamma . Coordinates of the centroid of the triangle ABC are
A. (−α/3,β/3,γ/3)( - \alpha /3,\beta /3,\gamma /3)
B. (α/3,−β/3,γ/3)(\alpha /3, - \beta /3,\gamma /3)
C. (α/3,β/3,−γ/3)(\alpha /3,\beta /3, - \gamma /3)
D. (α/3,β/3,γ/3)(\alpha /3,\beta /3,\gamma /3)

Explanation

Solution

A triangle ABC is placed so that the mid-points of the sides are on the x,y,z axes. Lengths of the intercepts made by the plane containing the triangle on these axes are respectivelyα,β,γ\alpha ,\beta ,\gamma . Coordinates of the centroid of the triangle ABC are
(−α/3,β/3,γ/3)( - \alpha /3,\beta /3,\gamma /3)
(α/3,−β/3,γ/3)(\alpha /3, - \beta /3,\gamma /3)
(α/3,β/3,−γ/3)(\alpha /3,\beta /3, - \gamma /3)
(α/3,β/3,γ/3)(\alpha /3,\beta /3,\gamma /3)

Complete step by step solution:

  1.  ABC\,ABC is placed so that the mid-points of the sides are on the x,y,z axes
    i.e.:D,E,F are the mid-points of CA , BC , BA respectively and D,E,F lie on the Z,Y,X axes.
  2. Lengths of the intercepts made by the plane containing the triangle on these axes are α,β,γ\alpha ,\beta ,\gamma respectively which means the coordinates of D,E,F are F(α,0,0),E(0,β,0)and D(0,0,γ)F(\alpha ,0,0),E(0,\beta ,0)and\,D(0,0,\gamma ).

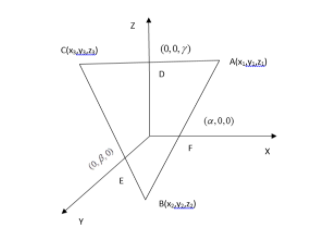
    Here, A=(x1,y1,z1)A = ({x_1},{y_1},{z_1})
    B=(x2,y2,z2)B = ({x_2},{y_2},{z_2})
    C=(x3,y3,z3)C = ({x_3},{y_3},{z_3})
    And F=(α,0,0)F = (\alpha ,0,0)
    E=(0,β,0)E = (0,\beta ,0)
    D=(0,0,γ)D = (0,0,\gamma )
    Step 1: To make a relation between the coordinates of A,B,C with α,β,γ\alpha ,\beta ,\gamma
    i)= > F=(x1+x22,y1+y22,z1+z22)F = (\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2},\dfrac{{{z_1} + {z_2}}}{2}) [ F is the mid point of AB]
    = > F=(α,0,0)F = (\alpha ,0,0)
    i.e.: x1+x22=α,  y1+y22=0,  z1+z22=0\dfrac{{{x_1} + {x_2}}}{2} = \alpha ,\,\,\dfrac{{{y_1} + {y_2}}}{2} = 0,\,\,\dfrac{{{z_1} + {z_2}}}{2} = 0
    ii) = > E=(x2+x32,y2+y32,z2+z32)E = (\dfrac{{{x_2} + {x_3}}}{2},\dfrac{{{y_2} + {y_3}}}{2},\dfrac{{{z_2} + {z_3}}}{2}) [ E is the mid point of BC]
    = > F=(0,β,0)F = (0,\beta ,0)
    i.e.: x2+x32=0,  y2+y32=β,  z2+z32=0\dfrac{{{x_2} + {x_3}}}{2} = 0,\,\,\dfrac{{{y_2} + {y_3}}}{2} = \beta ,\,\,\dfrac{{{z_2} + {z_3}}}{2} = 0
    => D=(x3+x12,y3+y12,z3+z12)D = (\dfrac{{{x_3} + {x_1}}}{2},\dfrac{{{y_3} + {y_1}}}{2},\dfrac{{{z_3} + {z_1}}}{2})
    = > D=(0,0,γ)D = (0,0,\gamma )
    i.e.: x3+x12=0,  y3+y12=0,  z3+z12=γ\dfrac{{{x_3} + {x_1}}}{2} = 0,\,\,\dfrac{{{y_3} + {y_1}}}{2} = 0,\,\,\dfrac{{{z_3} + {z_1}}}{2} = \gamma
    From (i) , We get,
    x1+x2=2α{x_1} + {x_2} = 2\alpha
    y1+y2=0{y_1} + {y_2} = 0
    z1+z2=0{z_1} + {z_2} = 0
    From (ii), we get,
    x2+x3=0{x_2} + {x_3} = 0
    y2+y3=2β{y_2} + {y_3} = 2\beta
    z2+z3=0{z_2} + {z_3} = 0
    From (iii), we get,
    x3+x1=0{x_3} + {x_1} = 0
    y3+y1=0{y_3} + {y_1} = 0
    z3+z1=2γ{z_3} + {z_1} = 2\gamma
    From all the above equations, we can conclude that,
    x1+x2+x3=α{x_1} + {x_2} + {x_3} = \alpha
    y1+y2+y3=β{y_1} + {y_2} + {y_3} = \beta
    z1+z2+z3=γ{z_1} + {z_2} + {z_3} = \gamma
    Hence, we get the coordinates of the points A,B,C in terms of α,β,γ\alpha ,\beta ,\gamma
    Step 2: We will now find out the coordinate of centroid of the triangle coordinate of the centroid of the triangle is given by
    (x1+x2+x33,y1+y2+y33,z1+z2+z33)(\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3},\dfrac{{{z_1} + {z_2} + {z_3}}}{3})
    = (α3,β3,γ3)(\dfrac{\alpha }{3},\dfrac{\beta }{3},\dfrac{\gamma }{3})
    Hence, the coordinate of the centroid of the triangle ABC is (α3,β3,γ3)(\dfrac{\alpha }{3},\dfrac{\beta }{3},\dfrac{\gamma }{3}).
    So, D(α3,β3,γ3)D(\dfrac{\alpha }{3},\dfrac{\beta }{3},\dfrac{\gamma }{3}) is the correct answer.

Note: Diagram should be drawn properly. As because, a correct diagram will only lead you to a correct answer. Also, equations should be written correctly.