Question

A triangle ABC has vertices A, B and C and its respective opposite sides have lengths a, b and c. This triangle ABC is inscribed in a circle of radius R. If b=c=1 and the altitude from A to side BC has length $\sqrt {\dfrac{2}{3}}$​​, then what is the value of R.
(A) $\sqrt 3$
(B) $\dfrac{{\sqrt 3 }}{{2\sqrt 2 }}$
(C) $\sqrt {\dfrac{1}{2}}$
(D) $\sqrt {\dfrac{1}{3}}$

Answer 1

Here it is given that b=c=1. This means it’s an isosceles triangle and height of the altitude is given from these we can find the area of the triangle $\Delta = \dfrac{1}{2} \times b \times h$ and find the value of a. As the triangle is inscribed in the circle so we apply the formula of circumradius $R = \dfrac{{a \times b \times c}}{{4 \times \Delta }}$ by solving this we get the value of R.

Complete step-by-step answer:

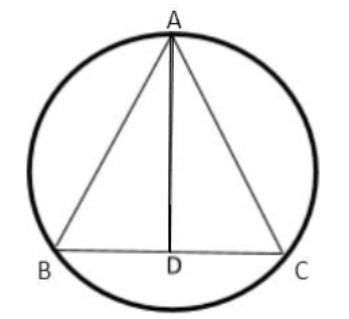
In fig AB=b, AC=c, BC=a , AD=$\sqrt {\dfrac{2}{3}}$
According to the question it is given that
b = c = 1,
So, the nature of the triangle is isosceles.
The length of the altitude AD = C,
Radius of the circle = R
Now we find the area of triangle ABC where BC is the base and AD is the height of the triangle
$\Delta = \dfrac{1}{2} \times b \times h$
$\Delta = \dfrac{1}{2} \times BC \times AD$
Now put the values BC=a , AD=$\sqrt {\dfrac{2}{3}}$, we get,
$\Delta = \dfrac{1}{2} \times a \times \sqrt {\dfrac{2}{3}}$
By solving we get value of a,
$a = 2 \times \Delta \times \sqrt {\dfrac{3}{2}}$
Now we find the circumradius of the circle in which triangle is inscribed
$R = \dfrac{{a \times b \times c}}{{4 \times \Delta }}$ where $\Delta$ is the area of the triangle.
We put the values of $a = 2 \times \Delta \times \sqrt {\dfrac{3}{2}}$,b=c=1 in the formula we get,
$\Rightarrow R = \dfrac{{(\dfrac{{2\Delta \sqrt 3 }}{{\sqrt 2 }}) \times 1 \times 1}}{{4 \times \Delta }}$
Now $\sqrt 2$ comes in the denominator,
$\Rightarrow R = \dfrac{{2 \times \Delta \times \sqrt 3 }}{{4 \times \sqrt 2 \times \Delta }}$
Now, We cancel out the similar terms
$\Rightarrow R = \dfrac{{\sqrt 2 \times \sqrt 2 \times \Delta \times \sqrt 3 }}{{2 \times 2 \times \sqrt 2 \times \Delta }}$
We get,
$\Rightarrow R = \dfrac{{\sqrt 3 }}{{2\sqrt 2 }}$
So, the circumradius of the circle$R = \dfrac{{\sqrt 3 }}{{2\sqrt 2 }}$.

So, the correct answer is “Option B”.

Note: The radius of circle circumscribed around a triangle is known as circumradius.Triangle inscribed in a circle means that there is a triangle which is drawn inside the circle. If it is a right angled triangle drawn inside a circle so its hypotenuse is the diameter of the circle.Students should remember formulas of area of triangle and circumradius for solving these types of questions.