Question

A tree stands vertical, on the hill side, which makes an angle of ${22^0}$with the horizontal. From the point 35 meters directly down the hill from the base of the tree, the angle of elevation of the top of the tree is ${45^0}$. Then the height of the tree (Given \sin \,{22^0}\, = \,0.3746,$$$$\cos \,{22^0}\, = \,0.9276from tables) is
A. 18.4 m
B. 20.4 m
C. 18.54 m
D. 30 m

Answer 1

The first and probably the most common use of trigonometry in the real world is the measuring of the height of a building or any other structure standing tall and it is to be done with the help of trigonometric ratios.
Trigonometric ratios are applicable only in a right angle triangle.
A right angle triangle includes a hypotenuse (the longest side), base, & the perpendicular.
Let a right angle triangle in $\vartriangle$ABC

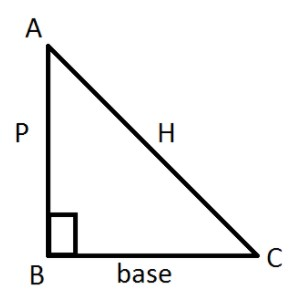
AB $=$ P, BC $=$ B, and AC $=$ H
Where P $=$ Perpendicular.
B $=$ Base.
H $=$ Hypotenuse.
Here, $\sin \theta = \dfrac{P}{H}$, $\tan \theta = \dfrac{P}{B}$, $\cos \theta = \dfrac{B}{H}$
$\cos ec\,\theta = \dfrac{H}{P}$, $\cot \,\theta = \dfrac{B}{P}$, $\sec \,\theta \, = \,\dfrac{H}{B}$.

Complete step by step solution:
Given,
$\sin \,{22^0} = 0.3746$, $\cos \,{22^0} = 0.9276$
Angle of elevation $= {45^0}$.
Let PQ be tree and A be the point on the ground AB:

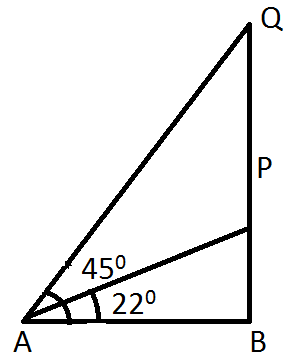
The tree PQ makes an angle of ${22^0}$with the horizontal AB
Hence, from A to P i.e. AP $= \,35$m because it is the distance directly down the hill from the base of the tree.
Now, $\angle QAB = {45^0}$_____(1), and $\angle PAB = {22^0}$
$\Rightarrow \angle PAQ = \angle QAB - \angle PAB$
$\Rightarrow \angle PAB = {45^0} - {22^0}$
$\Rightarrow \angle PAQ = {23^0}$
$\Rightarrow \angle AQP = {90^0} - \angle QAB$
$= {90^0} - {45^0} = {45^0}$ [From equation (1)].
Using sine rule in $\vartriangle QAP$ and $\vartriangle APB$ we get,
$\dfrac{{AP}}{{\sin \,{{45}^0}}} = \dfrac{{PQ}}{{\sin \,{{23}^0}}}$
$\dfrac{{35}}{{\dfrac{1}{{\sqrt 2 }}}} = \dfrac{{PQ}}{{\sin \,{{23}^0}}}$ [$\sin \,23 \cong \,\sin \,22 = 0.3746$]
$\dfrac{{35}}{{0.709}} = \dfrac{{PQ}}{{0.3746}}$
$PQ = \dfrac{{35 \times 0.3746}}{{0.709}} = 18.4$m.

Hence, the height of the tree is $18.4$m.

Note: Trigonometry is used to measure the height or a tree. The distance or the height can be measured with trigonometric ratios only.